Nonnegative CP Decomposition using Multiplicative Updates

>> Tensor Toolbox >> CP Decompositions >> CP-NMU

The function cp_nmu computes a nonnegative CP factorization using multiplicative updates. It does this using Lee & Seung multiplicative updates for nonnegative matrix/tensor factorization with a least squares objective function. The input X can be a tensor, sptensor, ktensor, or ttensor. The output CP model is a ktensor.

CP-NMU is a simple method for nonnegative CP decomposition and is not guaranteed to converge to a stationary point. Use CP-OPT with nonnegativity constraints for a more robust method.

Additionally, we have only implemented here the method for the least squares objective function. Use CP-APR for KL Divergence.

The CP-NMU method (for matrices) is described in:

D. D. Lee and H. S. Seung. Algorithms for Non-negative Matrix Factorization. Advances in Neural Information Processing Systems, 13, 2001. https://proceedings.neurips.cc/paper_files/paper/2000/hash/f9d1152547c0bde01830b7e8bd60024c-Abstract.html

Set up a sample problem
Run CP-NMU with default options
Run with custom initialization
Run with ktensor initialization
Trace option
Varying options

Set up a sample problem

We create a nonnegative tensor with a known solution and add a small amount of noise.

rng('default') % For reproducibility
sz = [30 25 20];
R = 3;
A = cell(3,1);
for n = 1:3
    A{n} = rand(sz(n), R);
end
lambda = rand(R,1);
S = ktensor(lambda, A);
X = full(S) + 0.01 * tensor(rand(sz));
M_true = S;

Run CP-NMU with default options

The default is random initialization and 500 iterations.

NOTE The random initialization uses random values in [0.1,1.1] to avoid zeros, which cause problems with the multiplicative updates.

rng('default') % For reproducibility
M = cp_nmu(X, R);
score_val = score(M, M_true);
fprintf('Score (run with default options): %.4f\n', score_val);

Nonnegative CP:
  tol = 0.0001,   maxiters = 500
  init = random
 Iter  1: fit = 9.103725e-01 fitdelta = 9.1e-01
 Iter  2: fit = 9.403600e-01 fitdelta = 3.0e-02
 Iter  3: fit = 9.501213e-01 fitdelta = 9.8e-03
 Iter  4: fit = 9.570217e-01 fitdelta = 6.9e-03
 Iter  5: fit = 9.619077e-01 fitdelta = 4.9e-03
 Iter  6: fit = 9.654248e-01 fitdelta = 3.5e-03
 Iter  7: fit = 9.680202e-01 fitdelta = 2.6e-03
 Iter  8: fit = 9.699901e-01 fitdelta = 2.0e-03
 Iter  9: fit = 9.715279e-01 fitdelta = 1.5e-03
 Iter 10: fit = 9.727606e-01 fitdelta = 1.2e-03
 Iter 11: fit = 9.737731e-01 fitdelta = 1.0e-03
 Iter 12: fit = 9.746231e-01 fitdelta = 8.5e-04
 Iter 13: fit = 9.753504e-01 fitdelta = 7.3e-04
 Iter 14: fit = 9.759834e-01 fitdelta = 6.3e-04
 Iter 15: fit = 9.765422e-01 fitdelta = 5.6e-04
 Iter 16: fit = 9.770416e-01 fitdelta = 5.0e-04
 Iter 17: fit = 9.774924e-01 fitdelta = 4.5e-04
 Iter 18: fit = 9.779027e-01 fitdelta = 4.1e-04
 Iter 19: fit = 9.782789e-01 fitdelta = 3.8e-04
 Iter 20: fit = 9.786255e-01 fitdelta = 3.5e-04
 Iter 21: fit = 9.789464e-01 fitdelta = 3.2e-04
 Iter 22: fit = 9.792445e-01 fitdelta = 3.0e-04
 Iter 23: fit = 9.795223e-01 fitdelta = 2.8e-04
 Iter 24: fit = 9.797818e-01 fitdelta = 2.6e-04
 Iter 25: fit = 9.800247e-01 fitdelta = 2.4e-04
 Iter 26: fit = 9.802525e-01 fitdelta = 2.3e-04
 Iter 27: fit = 9.804663e-01 fitdelta = 2.1e-04
 Iter 28: fit = 9.806673e-01 fitdelta = 2.0e-04
 Iter 29: fit = 9.808565e-01 fitdelta = 1.9e-04
 Iter 30: fit = 9.810347e-01 fitdelta = 1.8e-04
 Iter 31: fit = 9.812027e-01 fitdelta = 1.7e-04
 Iter 32: fit = 9.813613e-01 fitdelta = 1.6e-04
 Iter 33: fit = 9.815111e-01 fitdelta = 1.5e-04
 Iter 34: fit = 9.816527e-01 fitdelta = 1.4e-04
 Iter 35: fit = 9.817867e-01 fitdelta = 1.3e-04
 Iter 36: fit = 9.819135e-01 fitdelta = 1.3e-04
 Iter 37: fit = 9.820337e-01 fitdelta = 1.2e-04
 Iter 38: fit = 9.821477e-01 fitdelta = 1.1e-04
 Iter 39: fit = 9.822559e-01 fitdelta = 1.1e-04
 Iter 40: fit = 9.823586e-01 fitdelta = 1.0e-04
 Iter 41: fit = 9.824563e-01 fitdelta = 9.8e-05
 Final fit = 9.824563e-01 
Score (run with default options): 0.7675

Run with custom initialization

You can provide a cell array as the initial guess.

rng('default') % For reproducibility
Uinit = cell(3,1);
for n = 1:3
    Uinit{n} = rand(sz(n), R);
end
M1 = cp_nmu(X, R, 'init', Uinit, 'maxiters', 100);
score_val = score(M1, M_true);
fprintf('Score (run with custom init): %.4f\n', score_val);

Nonnegative CP:
  tol = 0.0001,   maxiters = 100
  init = cell
 Iter  1: fit = 9.141275e-01 fitdelta = 9.1e-01
 Iter  2: fit = 9.508846e-01 fitdelta = 3.7e-02
 Iter  3: fit = 9.585137e-01 fitdelta = 7.6e-03
 Iter  4: fit = 9.638050e-01 fitdelta = 5.3e-03
 Iter  5: fit = 9.676426e-01 fitdelta = 3.8e-03
 Iter  6: fit = 9.704992e-01 fitdelta = 2.9e-03
 Iter  7: fit = 9.726733e-01 fitdelta = 2.2e-03
 Iter  8: fit = 9.743614e-01 fitdelta = 1.7e-03
 Iter  9: fit = 9.756968e-01 fitdelta = 1.3e-03
 Iter 10: fit = 9.767722e-01 fitdelta = 1.1e-03
 Iter 11: fit = 9.776529e-01 fitdelta = 8.8e-04
 Iter 12: fit = 9.783857e-01 fitdelta = 7.3e-04
 Iter 13: fit = 9.790043e-01 fitdelta = 6.2e-04
 Iter 14: fit = 9.795338e-01 fitdelta = 5.3e-04
 Iter 15: fit = 9.799925e-01 fitdelta = 4.6e-04
 Iter 16: fit = 9.803942e-01 fitdelta = 4.0e-04
 Iter 17: fit = 9.807494e-01 fitdelta = 3.6e-04
 Iter 18: fit = 9.810662e-01 fitdelta = 3.2e-04
 Iter 19: fit = 9.813507e-01 fitdelta = 2.8e-04
 Iter 20: fit = 9.816079e-01 fitdelta = 2.6e-04
 Iter 21: fit = 9.818417e-01 fitdelta = 2.3e-04
 Iter 22: fit = 9.820553e-01 fitdelta = 2.1e-04
 Iter 23: fit = 9.822513e-01 fitdelta = 2.0e-04
 Iter 24: fit = 9.824318e-01 fitdelta = 1.8e-04
 Iter 25: fit = 9.825986e-01 fitdelta = 1.7e-04
 Iter 26: fit = 9.827532e-01 fitdelta = 1.5e-04
 Iter 27: fit = 9.828970e-01 fitdelta = 1.4e-04
 Iter 28: fit = 9.830309e-01 fitdelta = 1.3e-04
 Iter 29: fit = 9.831559e-01 fitdelta = 1.3e-04
 Iter 30: fit = 9.832730e-01 fitdelta = 1.2e-04
 Iter 31: fit = 9.833828e-01 fitdelta = 1.1e-04
 Iter 32: fit = 9.834859e-01 fitdelta = 1.0e-04
 Iter 33: fit = 9.835830e-01 fitdelta = 9.7e-05
 Final fit = 9.835830e-01 
Score (run with custom init): 0.7964

Run with ktensor initialization

Alternatively, you can pass in a ktensor as the initial guess. Here, I'm using the same factors as the custom initialization and the result will be the same.

kt_init = ktensor(Uinit);
M2 = cp_nmu(X, R, 'init', kt_init, 'maxiters', 100);
score_val = score(M2, M_true);
fprintf('Score (run with ktensor init): %.4f\n', score_val);

fprintf('Solutions equal? %d\n', isequal(M1, M2));

Nonnegative CP:
  tol = 0.0001,   maxiters = 100
  init = ktensor
 Iter  1: fit = 9.141275e-01 fitdelta = 9.1e-01
 Iter  2: fit = 9.508846e-01 fitdelta = 3.7e-02
 Iter  3: fit = 9.585137e-01 fitdelta = 7.6e-03
 Iter  4: fit = 9.638050e-01 fitdelta = 5.3e-03
 Iter  5: fit = 9.676426e-01 fitdelta = 3.8e-03
 Iter  6: fit = 9.704992e-01 fitdelta = 2.9e-03
 Iter  7: fit = 9.726733e-01 fitdelta = 2.2e-03
 Iter  8: fit = 9.743614e-01 fitdelta = 1.7e-03
 Iter  9: fit = 9.756968e-01 fitdelta = 1.3e-03
 Iter 10: fit = 9.767722e-01 fitdelta = 1.1e-03
 Iter 11: fit = 9.776529e-01 fitdelta = 8.8e-04
 Iter 12: fit = 9.783857e-01 fitdelta = 7.3e-04
 Iter 13: fit = 9.790043e-01 fitdelta = 6.2e-04
 Iter 14: fit = 9.795338e-01 fitdelta = 5.3e-04
 Iter 15: fit = 9.799925e-01 fitdelta = 4.6e-04
 Iter 16: fit = 9.803942e-01 fitdelta = 4.0e-04
 Iter 17: fit = 9.807494e-01 fitdelta = 3.6e-04
 Iter 18: fit = 9.810662e-01 fitdelta = 3.2e-04
 Iter 19: fit = 9.813507e-01 fitdelta = 2.8e-04
 Iter 20: fit = 9.816079e-01 fitdelta = 2.6e-04
 Iter 21: fit = 9.818417e-01 fitdelta = 2.3e-04
 Iter 22: fit = 9.820553e-01 fitdelta = 2.1e-04
 Iter 23: fit = 9.822513e-01 fitdelta = 2.0e-04
 Iter 24: fit = 9.824318e-01 fitdelta = 1.8e-04
 Iter 25: fit = 9.825986e-01 fitdelta = 1.7e-04
 Iter 26: fit = 9.827532e-01 fitdelta = 1.5e-04
 Iter 27: fit = 9.828970e-01 fitdelta = 1.4e-04
 Iter 28: fit = 9.830309e-01 fitdelta = 1.3e-04
 Iter 29: fit = 9.831559e-01 fitdelta = 1.3e-04
 Iter 30: fit = 9.832730e-01 fitdelta = 1.2e-04
 Iter 31: fit = 9.833828e-01 fitdelta = 1.1e-04
 Iter 32: fit = 9.834859e-01 fitdelta = 1.0e-04
 Iter 33: fit = 9.835830e-01 fitdelta = 9.7e-05
 Final fit = 9.835830e-01 
Score (run with ktensor init): 0.7964
Solutions equal? 1

Trace option

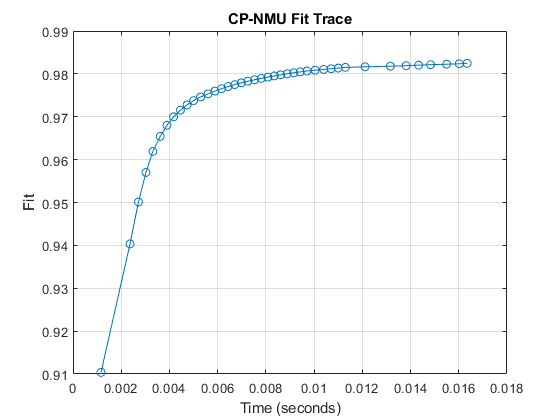
You can enable tracing to get fit and time per iteration.

rng('default') % For reproducibility
[M, ~, out] = cp_nmu(X, R, 'trace', true, 'maxiters', 50);
score_val = score(M, M_true);
fprintf('Score (run with default options): %.4f\n', score_val);
figure(1); clf;
plot(out.time_trace, out.fit_trace, '-o');
xlabel('Time (seconds)'); ylabel('Fit');
title('CP-NMU Fit Trace');
grid on;

Nonnegative CP:
  tol = 0.0001,   maxiters = 50
  init = random
  trace = true
 Iter  1: fit = 9.103725e-01 fitdelta = 9.1e-01
 Iter  2: fit = 9.403600e-01 fitdelta = 3.0e-02
 Iter  3: fit = 9.501213e-01 fitdelta = 9.8e-03
 Iter  4: fit = 9.570217e-01 fitdelta = 6.9e-03
 Iter  5: fit = 9.619077e-01 fitdelta = 4.9e-03
 Iter  6: fit = 9.654248e-01 fitdelta = 3.5e-03
 Iter  7: fit = 9.680202e-01 fitdelta = 2.6e-03
 Iter  8: fit = 9.699901e-01 fitdelta = 2.0e-03
 Iter  9: fit = 9.715279e-01 fitdelta = 1.5e-03
 Iter 10: fit = 9.727606e-01 fitdelta = 1.2e-03
 Iter 11: fit = 9.737731e-01 fitdelta = 1.0e-03
 Iter 12: fit = 9.746231e-01 fitdelta = 8.5e-04
 Iter 13: fit = 9.753504e-01 fitdelta = 7.3e-04
 Iter 14: fit = 9.759834e-01 fitdelta = 6.3e-04
 Iter 15: fit = 9.765422e-01 fitdelta = 5.6e-04
 Iter 16: fit = 9.770416e-01 fitdelta = 5.0e-04
 Iter 17: fit = 9.774924e-01 fitdelta = 4.5e-04
 Iter 18: fit = 9.779027e-01 fitdelta = 4.1e-04
 Iter 19: fit = 9.782789e-01 fitdelta = 3.8e-04
 Iter 20: fit = 9.786255e-01 fitdelta = 3.5e-04
 Iter 21: fit = 9.789464e-01 fitdelta = 3.2e-04
 Iter 22: fit = 9.792445e-01 fitdelta = 3.0e-04
 Iter 23: fit = 9.795223e-01 fitdelta = 2.8e-04
 Iter 24: fit = 9.797818e-01 fitdelta = 2.6e-04
 Iter 25: fit = 9.800247e-01 fitdelta = 2.4e-04
 Iter 26: fit = 9.802525e-01 fitdelta = 2.3e-04
 Iter 27: fit = 9.804663e-01 fitdelta = 2.1e-04
 Iter 28: fit = 9.806673e-01 fitdelta = 2.0e-04
 Iter 29: fit = 9.808565e-01 fitdelta = 1.9e-04
 Iter 30: fit = 9.810347e-01 fitdelta = 1.8e-04
 Iter 31: fit = 9.812027e-01 fitdelta = 1.7e-04
 Iter 32: fit = 9.813613e-01 fitdelta = 1.6e-04
 Iter 33: fit = 9.815111e-01 fitdelta = 1.5e-04
 Iter 34: fit = 9.816527e-01 fitdelta = 1.4e-04
 Iter 35: fit = 9.817867e-01 fitdelta = 1.3e-04
 Iter 36: fit = 9.819135e-01 fitdelta = 1.3e-04
 Iter 37: fit = 9.820337e-01 fitdelta = 1.2e-04
 Iter 38: fit = 9.821477e-01 fitdelta = 1.1e-04
 Iter 39: fit = 9.822559e-01 fitdelta = 1.1e-04
 Iter 40: fit = 9.823586e-01 fitdelta = 1.0e-04
 Iter 41: fit = 9.824563e-01 fitdelta = 9.8e-05
 Final fit = 9.824563e-01 
Score (run with default options): 0.7675

Varying options

You can change the order of updates or the tolerance or the maximum number of iterations.

rng('default') % For reproducibility
[M, U0, out] = cp_nmu(X, R, 'dimorder', [3 2 1], 'tol', 1e-5, 'maxiters', 100);
score_val = score(M, M_true);
fprintf('dimorder/tol score: %.4f\n', score_val);

Nonnegative CP:
  tol = 1e-05,   maxiters = 100
  dimorder = [3  2  1]
  init = random
 Iter  1: fit = 7.498676e-01 fitdelta = 7.5e-01
 Iter  2: fit = 7.715137e-01 fitdelta = 2.2e-02
 Iter  3: fit = 7.835071e-01 fitdelta = 1.2e-02
 Iter  4: fit = 7.927945e-01 fitdelta = 9.3e-03
 Iter  5: fit = 8.010841e-01 fitdelta = 8.3e-03
 Iter  6: fit = 8.094320e-01 fitdelta = 8.3e-03
 Iter  7: fit = 8.185604e-01 fitdelta = 9.1e-03
 Iter  8: fit = 8.289310e-01 fitdelta = 1.0e-02
 Iter  9: fit = 8.406978e-01 fitdelta = 1.2e-02
 Iter 10: fit = 8.536302e-01 fitdelta = 1.3e-02
 Iter 11: fit = 8.671246e-01 fitdelta = 1.3e-02
 Iter 12: fit = 8.803757e-01 fitdelta = 1.3e-02
 Iter 13: fit = 8.926376e-01 fitdelta = 1.2e-02
 Iter 14: fit = 9.034183e-01 fitdelta = 1.1e-02
 Iter 15: fit = 9.125253e-01 fitdelta = 9.1e-03
 Iter 16: fit = 9.200008e-01 fitdelta = 7.5e-03
 Iter 17: fit = 9.260252e-01 fitdelta = 6.0e-03
 Iter 18: fit = 9.308330e-01 fitdelta = 4.8e-03
 Iter 19: fit = 9.346593e-01 fitdelta = 3.8e-03
 Iter 20: fit = 9.377119e-01 fitdelta = 3.1e-03
 Iter 21: fit = 9.401617e-01 fitdelta = 2.4e-03
 Iter 22: fit = 9.421438e-01 fitdelta = 2.0e-03
 Iter 23: fit = 9.437629e-01 fitdelta = 1.6e-03
 Iter 24: fit = 9.450988e-01 fitdelta = 1.3e-03
 Iter 25: fit = 9.462122e-01 fitdelta = 1.1e-03
 Iter 26: fit = 9.471495e-01 fitdelta = 9.4e-04
 Iter 27: fit = 9.479463e-01 fitdelta = 8.0e-04
 Iter 28: fit = 9.486299e-01 fitdelta = 6.8e-04
 Iter 29: fit = 9.492213e-01 fitdelta = 5.9e-04
 Iter 30: fit = 9.497373e-01 fitdelta = 5.2e-04
 Iter 31: fit = 9.501908e-01 fitdelta = 4.5e-04
 Iter 32: fit = 9.505921e-01 fitdelta = 4.0e-04
 Iter 33: fit = 9.509495e-01 fitdelta = 3.6e-04
 Iter 34: fit = 9.512697e-01 fitdelta = 3.2e-04
 Iter 35: fit = 9.515581e-01 fitdelta = 2.9e-04
 Iter 36: fit = 9.518192e-01 fitdelta = 2.6e-04
 Iter 37: fit = 9.520566e-01 fitdelta = 2.4e-04
 Iter 38: fit = 9.522734e-01 fitdelta = 2.2e-04
 Iter 39: fit = 9.524721e-01 fitdelta = 2.0e-04
 Iter 40: fit = 9.526549e-01 fitdelta = 1.8e-04
 Iter 41: fit = 9.528236e-01 fitdelta = 1.7e-04
 Iter 42: fit = 9.529798e-01 fitdelta = 1.6e-04
 Iter 43: fit = 9.531247e-01 fitdelta = 1.4e-04
 Iter 44: fit = 9.532597e-01 fitdelta = 1.3e-04
 Iter 45: fit = 9.533855e-01 fitdelta = 1.3e-04
 Iter 46: fit = 9.535032e-01 fitdelta = 1.2e-04
 Iter 47: fit = 9.536134e-01 fitdelta = 1.1e-04
 Iter 48: fit = 9.537169e-01 fitdelta = 1.0e-04
 Iter 49: fit = 9.538141e-01 fitdelta = 9.7e-05
 Iter 50: fit = 9.539058e-01 fitdelta = 9.2e-05
 Iter 51: fit = 9.539922e-01 fitdelta = 8.6e-05
 Iter 52: fit = 9.540739e-01 fitdelta = 8.2e-05
 Iter 53: fit = 9.541512e-01 fitdelta = 7.7e-05
 Iter 54: fit = 9.542245e-01 fitdelta = 7.3e-05
 Iter 55: fit = 9.542940e-01 fitdelta = 7.0e-05
 Iter 56: fit = 9.543600e-01 fitdelta = 6.6e-05
 Iter 57: fit = 9.544228e-01 fitdelta = 6.3e-05
 Iter 58: fit = 9.544826e-01 fitdelta = 6.0e-05
 Iter 59: fit = 9.545397e-01 fitdelta = 5.7e-05
 Iter 60: fit = 9.545941e-01 fitdelta = 5.4e-05
 Iter 61: fit = 9.546461e-01 fitdelta = 5.2e-05
 Iter 62: fit = 9.546959e-01 fitdelta = 5.0e-05
 Iter 63: fit = 9.547435e-01 fitdelta = 4.8e-05
 Iter 64: fit = 9.547892e-01 fitdelta = 4.6e-05
 Iter 65: fit = 9.548331e-01 fitdelta = 4.4e-05
 Iter 66: fit = 9.548752e-01 fitdelta = 4.2e-05
 Iter 67: fit = 9.549157e-01 fitdelta = 4.1e-05
 Iter 68: fit = 9.549547e-01 fitdelta = 3.9e-05
 Iter 69: fit = 9.549923e-01 fitdelta = 3.8e-05
 Iter 70: fit = 9.550286e-01 fitdelta = 3.6e-05
 Iter 71: fit = 9.550636e-01 fitdelta = 3.5e-05
 Iter 72: fit = 9.550975e-01 fitdelta = 3.4e-05
 Iter 73: fit = 9.551303e-01 fitdelta = 3.3e-05
 Iter 74: fit = 9.551621e-01 fitdelta = 3.2e-05
 Iter 75: fit = 9.551930e-01 fitdelta = 3.1e-05
 Iter 76: fit = 9.552229e-01 fitdelta = 3.0e-05
 Iter 77: fit = 9.552521e-01 fitdelta = 2.9e-05
 Iter 78: fit = 9.552805e-01 fitdelta = 2.8e-05
 Iter 79: fit = 9.553082e-01 fitdelta = 2.8e-05
 Iter 80: fit = 9.553352e-01 fitdelta = 2.7e-05
 Iter 81: fit = 9.553617e-01 fitdelta = 2.6e-05
 Iter 82: fit = 9.553876e-01 fitdelta = 2.6e-05
 Iter 83: fit = 9.554130e-01 fitdelta = 2.5e-05
 Iter 84: fit = 9.554380e-01 fitdelta = 2.5e-05
 Iter 85: fit = 9.554626e-01 fitdelta = 2.5e-05
 Iter 86: fit = 9.554868e-01 fitdelta = 2.4e-05
 Iter 87: fit = 9.555108e-01 fitdelta = 2.4e-05
 Iter 88: fit = 9.555344e-01 fitdelta = 2.4e-05
 Iter 89: fit = 9.555579e-01 fitdelta = 2.3e-05
 Iter 90: fit = 9.555812e-01 fitdelta = 2.3e-05
 Iter 91: fit = 9.556044e-01 fitdelta = 2.3e-05
 Iter 92: fit = 9.556275e-01 fitdelta = 2.3e-05
 Iter 93: fit = 9.556506e-01 fitdelta = 2.3e-05
 Iter 94: fit = 9.556737e-01 fitdelta = 2.3e-05
 Iter 95: fit = 9.556969e-01 fitdelta = 2.3e-05
 Iter 96: fit = 9.557202e-01 fitdelta = 2.3e-05
 Iter 97: fit = 9.557436e-01 fitdelta = 2.3e-05
 Iter 98: fit = 9.557673e-01 fitdelta = 2.4e-05
 Iter 99: fit = 9.557913e-01 fitdelta = 2.4e-05
 Iter 100: fit = 9.558156e-01 fitdelta = 2.4e-05
 Final fit = 9.558156e-01 
dimorder/tol score: 0.5331