Alternating Poisson Regression for fitting CP to sparse count data

>> Tensor Toolbox >> CP Decompositions >> CP-APR

References:

E. C. Chi, T. G. Kolda, On Tensors, Sparsity, and Nonnegative Factorizations, SIAM J. Matrix Analysis and Applications, 33:1272-1299, 2012, https://doi.org/10.1137/110859063
S. Hansen, T. Plantenga and T. G. Kolda, Newton-Based Optimization for Kullback-Leibler Nonnegative Tensor Factorizations, Optimization Methods and Software, 30(5):955-979, 2015, http://dx.doi.org/10.1080/10556788.2015.1009977

Set up a sample problem
Call CP-APR
Example using the 'pdnr' algorithm
Example using the 'mu' algorithm
Comparing results
Visualize the results

Set up a sample problem

We follow the general procedure for creating a problem outlined by Chi and Kolda (2012). This creates a sparse count tensor with a known solution. The solution is a CP decomposition with a few large entries in each column of the factor matrices. The solution is normalized and sorted by component size in descending order.

rng('default') %<- Setting random seed for reproducibility of this script

% Pick the size and rank
sz = [100 80 60];
R = 5;

% Generate factor matrices with a few large entries in each column; this
% will be the basis of our soln.
A = cell(3,1);
for n = 1:length(sz)
    A{n} = rand(sz(n), R);
    for r = 1:R
        p = randperm(sz(n));
        nbig = round( (1/R)*sz(n) );
        A{n}(p(1:nbig),r) = 100 * A{n}(p(1:nbig),r);
    end
end
lambda = rand(R,1);
S = ktensor(lambda, A);
S = normalize(S,'sort',1);

% Create sparse test problem based on provided solution.
nz = prod(sz) * .05;
info = create_problem('Soln', S, 'Sparse_Generation', nz);

% Extract data and solution
X = info.Data;
M_true = info.Soln;

Call CP-APR

Alternating Poisson Regression (APR) is a method for fitting a CP decomposition to sparse count data. It is a nonnegative method that minimizes the Kullback-Leibler divergence between the data and the model. The method is implemented in the cp_apr function, which is similar to the cp_als function, but uses a different objective function and optimization method. The cp_apr function is designed to handle sparse count data and is particularly useful for fitting nonnegative CP decompositions.

The cp_apr function is a wrapper that calls one of three specific algorithms, selected by the 'alg' parameter:

'pqnr' (Default): Row subproblems are solved by Projected Quasi-Newton with L-BFGS. This method generally offers a good balance of speed and robustness and is suitable for a wide range of problems. It approximates the Hessian using gradient information from previous iterations. It is based on the work by Hansen, Plantenga, and Kolda (2015).
'pdnr': Row subproblems are solved by Projected Damped Newton. This method uses the exact Hessian for the row subproblems, which can lead to higher accuracy per iteration but may be more computationally intensive, especially for large R, as it involves forming and solving an R x R system at each inner iteration for each row. It is based on the work by Hansen, Plantenga, and Kolda (2015).
'mu': Multiplicative Update. This is a simpler algorithm, often with cheaper iterations. It can be slower to converge to high accuracy compared to Newton-based methods but can be effective for very large, sparse problems or for obtaining an initial guess quickly. It is based on the work by Chi & Kolda (2012).

The following example uses the default 'pqnr' algorithm. We run the method 5 times and keep the best solution (lowest objective value).

% Compute a solution using the default 'pqnr' algorithm
fprintf('--- Running CP-APR with PQNR (default) ---\n');
rng('default')
best_obj = inf;
for trial = 1:5
    [M_tmp,~,output_tmp] = cp_apr(X, R, 'printitn', 2);
    if output_tmp.obj < best_obj
        best_obj = output_tmp.obj;
        M_pqnr = M_tmp;
        output_pqnr = output_tmp;
    end
end

% Score the solution (a score of 1 is perfect)
factor_match_score_pqnr = score(M_pqnr, M_true, 'greedy', true);

--- Running CP-APR with PQNR (default) ---

CP_APR:

 Tensor size = [100 80 60], Approximation Rank = 5
 Tensor type: sparse with 10450 (2.2%) nonzeros 
 alg = 'pqnr' (quasi-Newton)
 stoptol = 0.0001, stoptime = 1e+06
 maxiters = 1000, maxinneriters = 10
 epsDivZero = 1e-10, epsActive = 1e-08
 precompinds = 1

 Precomputing sparse index sets...done
   2. Ttl Inner Its: 2370, KKT viol = 3.72e+00, obj = 1.64937774e+04, nz: 271
   4. Ttl Inner Its: 2164, KKT viol = 1.81e+00, obj = 1.26971895e+04, nz: 249
   6. Ttl Inner Its: 1742, KKT viol = 5.75e-01, obj = 1.25597728e+04, nz: 276
   8. Ttl Inner Its: 1148, KKT viol = 4.01e-02, obj = 1.25592937e+04, nz: 279
  10. Ttl Inner Its: 488, KKT viol = 7.84e-03, obj = 1.25592875e+04, nz: 280
  12. Ttl Inner Its: 293, KKT viol = 3.86e-03, obj = 1.25592870e+04, nz: 280
  14. Ttl Inner Its: 273, KKT viol = 1.96e-03, obj = 1.25592869e+04, nz: 280
  16. Ttl Inner Its: 249, KKT viol = 9.17e-04, obj = 1.25592869e+04, nz: 280
  18. Ttl Inner Its: 246, KKT viol = 4.78e-04, obj = 1.25592869e+04, nz: 280
  20. Ttl Inner Its: 242, KKT viol = 1.94e-04, obj = 1.25592869e+04, nz: 280
  22. Ttl Inner Its: 241, KKT viol = 1.09e-04, obj = 1.25592869e+04, nz: 280
===========================================
 Final f = 1.255929e+04 
 Final least squares fit = 5.232288e-01 
 Final KKT violation = 9.8366707e-05
 Total inner iterations = 20219
 Total execution time = 1.12 secs

CP_APR:

 Tensor size = [100 80 60], Approximation Rank = 5
 Tensor type: sparse with 10450 (2.2%) nonzeros 
 alg = 'pqnr' (quasi-Newton)
 stoptol = 0.0001, stoptime = 1e+06
 maxiters = 1000, maxinneriters = 10
 epsDivZero = 1e-10, epsActive = 1e-08
 precompinds = 1

 Precomputing sparse index sets...done
   2. Ttl Inner Its: 2364, KKT viol = 4.77e+00, obj = 1.74548483e+04, nz: 321
   4. Ttl Inner Its: 2282, KKT viol = 2.35e+00, obj = 1.48353911e+04, nz: 283
   6. Ttl Inner Its: 2083, KKT viol = 4.68e-01, obj = 1.44062370e+04, nz: 276
   8. Ttl Inner Its: 1814, KKT viol = 1.11e-01, obj = 1.43840303e+04, nz: 287
  10. Ttl Inner Its: 1649, KKT viol = 2.49e-01, obj = 1.43731087e+04, nz: 290
  12. Ttl Inner Its: 1579, KKT viol = 1.75e-01, obj = 1.43671444e+04, nz: 291
  14. Ttl Inner Its: 1304, KKT viol = 6.69e-02, obj = 1.43656031e+04, nz: 295
  16. Ttl Inner Its: 1338, KKT viol = 1.50e-01, obj = 1.43641731e+04, nz: 293
  18. Ttl Inner Its: 1355, KKT viol = 6.13e-02, obj = 1.43621016e+04, nz: 296
  20. Ttl Inner Its: 1264, KKT viol = 4.25e-02, obj = 1.43611481e+04, nz: 302
  22. Ttl Inner Its: 953, KKT viol = 4.40e-02, obj = 1.43609727e+04, nz: 306
  24. Ttl Inner Its: 894, KKT viol = 3.46e-02, obj = 1.43608920e+04, nz: 306
  26. Ttl Inner Its: 1007, KKT viol = 3.55e-02, obj = 1.43608107e+04, nz: 306
  28. Ttl Inner Its: 865, KKT viol = 5.94e-03, obj = 1.43607903e+04, nz: 307
  30. Ttl Inner Its: 724, KKT viol = 3.37e-03, obj = 1.43607868e+04, nz: 306
  32. Ttl Inner Its: 552, KKT viol = 1.94e-03, obj = 1.43607858e+04, nz: 306
  34. Ttl Inner Its: 414, KKT viol = 8.77e-04, obj = 1.43607854e+04, nz: 306
  36. Ttl Inner Its: 314, KKT viol = 5.43e-04, obj = 1.43607853e+04, nz: 306
  38. Ttl Inner Its: 258, KKT viol = 1.82e-04, obj = 1.43607853e+04, nz: 306
  40. Ttl Inner Its: 247, KKT viol = 1.23e-04, obj = 1.43607853e+04, nz: 306
===========================================
 Final f = 1.436079e+04 
 Final least squares fit = 5.160188e-01 
 Final KKT violation = 9.5163112e-05
 Total inner iterations = 47847
 Total execution time = 2.11 secs

CP_APR:

 Tensor size = [100 80 60], Approximation Rank = 5
 Tensor type: sparse with 10450 (2.2%) nonzeros 
 alg = 'pqnr' (quasi-Newton)
 stoptol = 0.0001, stoptime = 1e+06
 maxiters = 1000, maxinneriters = 10
 epsDivZero = 1e-10, epsActive = 1e-08
 precompinds = 1

 Precomputing sparse index sets...done
   2. Ttl Inner Its: 2354, KKT viol = 6.59e+00, obj = 1.37026077e+04, nz: 263
   4. Ttl Inner Its: 1997, KKT viol = 7.56e-01, obj = 1.25681246e+04, nz: 267
   6. Ttl Inner Its: 1567, KKT viol = 1.62e-01, obj = 1.25599271e+04, nz: 278
   8. Ttl Inner Its: 698, KKT viol = 3.90e-02, obj = 1.25598567e+04, nz: 278
  10. Ttl Inner Its: 464, KKT viol = 2.07e-02, obj = 1.25598465e+04, nz: 278
  12. Ttl Inner Its: 313, KKT viol = 1.07e-02, obj = 1.25598437e+04, nz: 279
  14. Ttl Inner Its: 314, KKT viol = 5.39e-03, obj = 1.25598430e+04, nz: 279
  16. Ttl Inner Its: 263, KKT viol = 2.70e-03, obj = 1.25598428e+04, nz: 279
  18. Ttl Inner Its: 254, KKT viol = 1.36e-03, obj = 1.25598428e+04, nz: 279
  20. Ttl Inner Its: 248, KKT viol = 6.69e-04, obj = 1.25598428e+04, nz: 279
  22. Ttl Inner Its: 247, KKT viol = 3.47e-04, obj = 1.25598428e+04, nz: 279
  24. Ttl Inner Its: 242, KKT viol = 1.40e-04, obj = 1.25598428e+04, nz: 279
  26. Ttl Inner Its: 240, KKT viol = 9.82e-05, obj = 1.25598427e+04, nz: 279
===========================================
 Final f = 1.255984e+04 
 Final least squares fit = 5.232265e-01 
 Final KKT violation = 9.8211173e-05
 Total inner iterations = 19446
 Total execution time = 1.14 secs

CP_APR:

 Tensor size = [100 80 60], Approximation Rank = 5
 Tensor type: sparse with 10450 (2.2%) nonzeros 
 alg = 'pqnr' (quasi-Newton)
 stoptol = 0.0001, stoptime = 1e+06
 maxiters = 1000, maxinneriters = 10
 epsDivZero = 1e-10, epsActive = 1e-08
 precompinds = 1

 Precomputing sparse index sets...done
   2. Ttl Inner Its: 2359, KKT viol = 3.34e+04, obj = 1.54901159e+04, nz: 266
   4. Ttl Inner Its: 2119, KKT viol = 1.00e+00, obj = 1.44274757e+04, nz: 283
   6. Ttl Inner Its: 1812, KKT viol = 2.61e-01, obj = 1.43754371e+04, nz: 288
   8. Ttl Inner Its: 1586, KKT viol = 1.98e-01, obj = 1.43684214e+04, nz: 293
  10. Ttl Inner Its: 1478, KKT viol = 1.37e-01, obj = 1.43646587e+04, nz: 299
  12. Ttl Inner Its: 1411, KKT viol = 1.96e-01, obj = 1.43596863e+04, nz: 303
  14. Ttl Inner Its: 1467, KKT viol = 2.05e-01, obj = 1.43566765e+04, nz: 296
  16. Ttl Inner Its: 1660, KKT viol = 3.69e-01, obj = 1.43401947e+04, nz: 286
  18. Ttl Inner Its: 2019, KKT viol = 2.19e+00, obj = 1.33546642e+04, nz: 265
  20. Ttl Inner Its: 1891, KKT viol = 9.14e-01, obj = 1.25614742e+04, nz: 274
  22. Ttl Inner Its: 1062, KKT viol = 3.59e-02, obj = 1.25593464e+04, nz: 279
  24. Ttl Inner Its: 439, KKT viol = 8.91e-03, obj = 1.25593396e+04, nz: 280
  26. Ttl Inner Its: 312, KKT viol = 4.40e-03, obj = 1.25593389e+04, nz: 281
  28. Ttl Inner Its: 277, KKT viol = 2.27e-03, obj = 1.25593388e+04, nz: 281
  30. Ttl Inner Its: 250, KKT viol = 1.09e-03, obj = 1.25593388e+04, nz: 281
  32. Ttl Inner Its: 244, KKT viol = 5.31e-04, obj = 1.25593388e+04, nz: 281
  34. Ttl Inner Its: 244, KKT viol = 2.94e-04, obj = 1.25593388e+04, nz: 281
  36. Ttl Inner Its: 243, KKT viol = 1.25e-04, obj = 1.25593388e+04, nz: 281
===========================================
 Final f = 1.255934e+04 
 Final least squares fit = 5.232254e-01 
 Final KKT violation = 9.5937950e-05
 Total inner iterations = 42943
 Total execution time = 2.20 secs

CP_APR:

 Tensor size = [100 80 60], Approximation Rank = 5
 Tensor type: sparse with 10450 (2.2%) nonzeros 
 alg = 'pqnr' (quasi-Newton)
 stoptol = 0.0001, stoptime = 1e+06
 maxiters = 1000, maxinneriters = 10
 epsDivZero = 1e-10, epsActive = 1e-08
 precompinds = 1

 Precomputing sparse index sets...done
   2. Ttl Inner Its: 2362, KKT viol = 4.33e+00, obj = 1.61058863e+04, nz: 261
   4. Ttl Inner Its: 2187, KKT viol = 1.78e+00, obj = 1.30304826e+04, nz: 264
   6. Ttl Inner Its: 1922, KKT viol = 9.02e-01, obj = 1.25620840e+04, nz: 273
   8. Ttl Inner Its: 1422, KKT viol = 8.22e-02, obj = 1.25593143e+04, nz: 278
  10. Ttl Inner Its: 524, KKT viol = 1.25e-02, obj = 1.25592873e+04, nz: 280
  12. Ttl Inner Its: 303, KKT viol = 2.70e-03, obj = 1.25592869e+04, nz: 280
  14. Ttl Inner Its: 258, KKT viol = 1.36e-03, obj = 1.25592869e+04, nz: 280
  16. Ttl Inner Its: 252, KKT viol = 6.63e-04, obj = 1.25592869e+04, nz: 280
  18. Ttl Inner Its: 244, KKT viol = 3.32e-04, obj = 1.25592869e+04, nz: 280
  20. Ttl Inner Its: 244, KKT viol = 1.52e-04, obj = 1.25592869e+04, nz: 280
===========================================
 Final f = 1.255929e+04 
 Final least squares fit = 5.232290e-01 
 Final KKT violation = 9.5799877e-05
 Total inner iterations = 20721
 Total execution time = 1.13 secs

Example using the 'pdnr' algorithm

Here, we explicitly select the 'pdnr' algorithm. We also reduce the maximum number of iterations for this demonstration. We run the method 5 times and keep the best solution (lowest objective value).

fprintf('--- Running CP-APR with PDNR ---\n');
rng('default')
best_obj_pdnr = inf;
for trial = 1:5
    [M_tmp,~,output_tmp] = cp_apr(X, R, 'alg', 'pdnr', 'printitn', 2);
    if output_tmp.obj < best_obj_pdnr
        best_obj_pdnr = output_tmp.obj;
        M_pdnr = M_tmp;
        output_pdnr = output_tmp;
    end
end

% Score the solution
factor_match_score_pdnr = score(M_pdnr, M_true, 'greedy', true);

--- Running CP-APR with PDNR ---

CP_APR:

 Tensor size = [100 80 60], Approximation Rank = 5
 Tensor type: sparse with 10450 (2.2%) nonzeros 
 alg = 'pdnr' (damped Newton)
 stoptol = 0.0001, stoptime = 1e+06
 maxiters = 1000, maxinneriters = 10
 epsDivZero = 1e-10, epsActive = 1e-08
 mu0 = 1e-05, inexact = 1
 precompinds = 1

 Precomputing sparse index sets...done
   2. Ttl Inner Its: 1224, KKT viol = 8.10e+02, obj = 2.08873010e+04, nz: 340
   4. Ttl Inner Its: 240, KKT viol = 7.86e+00, obj = 2.04610219e+04, nz: 309
   6. Ttl Inner Its: 294, KKT viol = 4.67e+01, obj = 1.73189096e+04, nz: 307
   8. Ttl Inner Its: 640, KKT viol = 3.51e+00, obj = 1.66981705e+04, nz: 308
  10. Ttl Inner Its: 263, KKT viol = 5.21e+01, obj = 1.45105514e+04, nz: 279
  12. Ttl Inner Its: 544, KKT viol = 1.89e+00, obj = 1.43716675e+04, nz: 297
  14. Ttl Inner Its: 391, KKT viol = 2.31e-01, obj = 1.43653907e+04, nz: 297
  16. Ttl Inner Its: 431, KKT viol = 4.82e-02, obj = 1.43640168e+04, nz: 298
  18. Ttl Inner Its: 478, KKT viol = 2.09e-01, obj = 1.43626771e+04, nz: 300
  20. Ttl Inner Its: 470, KKT viol = 2.70e-02, obj = 1.43617928e+04, nz: 301
  22. Ttl Inner Its: 464, KKT viol = 6.34e-02, obj = 1.43611589e+04, nz: 301
  24. Ttl Inner Its: 465, KKT viol = 3.30e-02, obj = 1.43605962e+04, nz: 304
  26. Ttl Inner Its: 474, KKT viol = 2.68e-02, obj = 1.43603417e+04, nz: 301
  28. Ttl Inner Its: 473, KKT viol = 8.16e-02, obj = 1.43601599e+04, nz: 299
  30. Ttl Inner Its: 440, KKT viol = 1.03e-01, obj = 1.43596476e+04, nz: 301
  32. Ttl Inner Its: 451, KKT viol = 8.07e-02, obj = 1.43590520e+04, nz: 302
  34. Ttl Inner Its: 464, KKT viol = 2.28e-01, obj = 1.43580597e+04, nz: 302
  36. Ttl Inner Its: 484, KKT viol = 4.16e-02, obj = 1.43576430e+04, nz: 300
  38. Ttl Inner Its: 474, KKT viol = 4.23e-02, obj = 1.43572954e+04, nz: 299
  40. Ttl Inner Its: 478, KKT viol = 4.78e-02, obj = 1.43569118e+04, nz: 295
  42. Ttl Inner Its: 489, KKT viol = 1.14e-01, obj = 1.43557419e+04, nz: 295
  44. Ttl Inner Its: 505, KKT viol = 1.51e-01, obj = 1.43524794e+04, nz: 292
  46. Ttl Inner Its: 471, KKT viol = 1.04e+00, obj = 1.43477325e+04, nz: 292
  48. Ttl Inner Its: 408, KKT viol = 2.67e-02, obj = 1.43466268e+04, nz: 294
  50. Ttl Inner Its: 470, KKT viol = 2.72e-02, obj = 1.43463649e+04, nz: 294
  52. Ttl Inner Its: 468, KKT viol = 2.60e-02, obj = 1.43462201e+04, nz: 294
  54. Ttl Inner Its: 465, KKT viol = 2.40e-02, obj = 1.43461180e+04, nz: 293
  56. Ttl Inner Its: 471, KKT viol = 1.54e-02, obj = 1.43460584e+04, nz: 293
  58. Ttl Inner Its: 469, KKT viol = 1.49e-02, obj = 1.43460250e+04, nz: 292
  60. Ttl Inner Its: 463, KKT viol = 1.45e-02, obj = 1.43459990e+04, nz: 292
  62. Ttl Inner Its: 469, KKT viol = 9.39e-03, obj = 1.43459796e+04, nz: 293
  64. Ttl Inner Its: 466, KKT viol = 6.91e-03, obj = 1.43459683e+04, nz: 293
  66. Ttl Inner Its: 462, KKT viol = 5.11e-03, obj = 1.43459622e+04, nz: 293
  68. Ttl Inner Its: 462, KKT viol = 3.63e-03, obj = 1.43459589e+04, nz: 292
  70. Ttl Inner Its: 459, KKT viol = 2.55e-03, obj = 1.43459570e+04, nz: 292
  72. Ttl Inner Its: 454, KKT viol = 1.80e-03, obj = 1.43459559e+04, nz: 292
  74. Ttl Inner Its: 437, KKT viol = 1.20e-03, obj = 1.43459553e+04, nz: 292
  76. Ttl Inner Its: 392, KKT viol = 8.44e-04, obj = 1.43459550e+04, nz: 292
  78. Ttl Inner Its: 345, KKT viol = 4.35e-04, obj = 1.43459549e+04, nz: 292
  80. Ttl Inner Its: 282, KKT viol = 2.61e-04, obj = 1.43459548e+04, nz: 292
  82. Ttl Inner Its: 264, KKT viol = 2.27e-04, obj = 1.43459548e+04, nz: 292
  84. Ttl Inner Its: 271, KKT viol = 3.03e-04, obj = 1.43459547e+04, nz: 292
  86. Ttl Inner Its: 240, KKT viol = 9.94e-05, obj = 1.43459547e+04, nz: 292
===========================================
 Final f = 1.434595e+04 
 Final least squares fit = 5.147296e-01 
 Final KKT violation = 9.9407836e-05
 Total inner iterations = 39250
 Total execution time = 4.40 secs

CP_APR:

 Tensor size = [100 80 60], Approximation Rank = 5
 Tensor type: sparse with 10450 (2.2%) nonzeros 
 alg = 'pdnr' (damped Newton)
 stoptol = 0.0001, stoptime = 1e+06
 maxiters = 1000, maxinneriters = 10
 epsDivZero = 1e-10, epsActive = 1e-08
 mu0 = 1e-05, inexact = 1
 precompinds = 1

 Precomputing sparse index sets...done
   2. Ttl Inner Its: 620, KKT viol = 1.87e+03, obj = 3.72481432e+04, nz: 327
   4. Ttl Inner Its: 1082, KKT viol = 5.42e+01, obj = 1.71493242e+04, nz: 325
   6. Ttl Inner Its: 245, KKT viol = 6.15e+01, obj = 1.30919319e+04, nz: 263
   8. Ttl Inner Its: 643, KKT viol = 9.41e-01, obj = 1.25717033e+04, nz: 275
  10. Ttl Inner Its: 300, KKT viol = 4.10e-01, obj = 1.25598716e+04, nz: 278
  12. Ttl Inner Its: 325, KKT viol = 4.34e-02, obj = 1.25597842e+04, nz: 279
  14. Ttl Inner Its: 335, KKT viol = 1.30e-02, obj = 1.25597785e+04, nz: 279
  16. Ttl Inner Its: 303, KKT viol = 4.89e-03, obj = 1.25597781e+04, nz: 280
  18. Ttl Inner Its: 253, KKT viol = 2.41e-03, obj = 1.25597781e+04, nz: 280
  20. Ttl Inner Its: 251, KKT viol = 1.20e-03, obj = 1.25597781e+04, nz: 280
  22. Ttl Inner Its: 244, KKT viol = 5.73e-04, obj = 1.25597781e+04, nz: 280
  24. Ttl Inner Its: 244, KKT viol = 2.64e-04, obj = 1.25597781e+04, nz: 280
  26. Ttl Inner Its: 244, KKT viol = 1.50e-04, obj = 1.25597781e+04, nz: 280
  28. Ttl Inner Its: 240, KKT viol = 9.97e-05, obj = 1.25597781e+04, nz: 280
===========================================
 Final f = 1.255978e+04 
 Final least squares fit = 5.232344e-01 
 Final KKT violation = 9.9668454e-05
 Total inner iterations = 10401
 Total execution time = 1.08 secs

CP_APR:

 Tensor size = [100 80 60], Approximation Rank = 5
 Tensor type: sparse with 10450 (2.2%) nonzeros 
 alg = 'pdnr' (damped Newton)
 stoptol = 0.0001, stoptime = 1e+06
 maxiters = 1000, maxinneriters = 10
 epsDivZero = 1e-10, epsActive = 1e-08
 mu0 = 1e-05, inexact = 1
 precompinds = 1

 Precomputing sparse index sets...done
   2. Ttl Inner Its: 521, KKT viol = 1.58e+03, obj = 3.57843712e+04, nz: 325
   4. Ttl Inner Its: 1013, KKT viol = 4.47e+01, obj = 1.83420068e+04, nz: 342
   6. Ttl Inner Its: 240, KKT viol = 2.83e+00, obj = 1.71814960e+04, nz: 296
   8. Ttl Inner Its: 524, KKT viol = 1.71e+00, obj = 1.68610010e+04, nz: 318
  10. Ttl Inner Its: 727, KKT viol = 2.25e+02, obj = 1.44014052e+04, nz: 290
  12. Ttl Inner Its: 463, KKT viol = 2.06e+00, obj = 1.42891949e+04, nz: 287
  14. Ttl Inner Its: 802, KKT viol = 4.34e+01, obj = 1.26000219e+04, nz: 269
  16. Ttl Inner Its: 371, KKT viol = 6.95e-01, obj = 1.25640961e+04, nz: 278
  18. Ttl Inner Its: 328, KKT viol = 1.76e-01, obj = 1.25593059e+04, nz: 278
  20. Ttl Inner Its: 346, KKT viol = 1.42e-02, obj = 1.25592875e+04, nz: 280
  22. Ttl Inner Its: 322, KKT viol = 6.92e-03, obj = 1.25592870e+04, nz: 280
  24. Ttl Inner Its: 261, KKT viol = 3.43e-03, obj = 1.25592869e+04, nz: 280
  26. Ttl Inner Its: 247, KKT viol = 1.68e-03, obj = 1.25592868e+04, nz: 280
  28. Ttl Inner Its: 246, KKT viol = 7.81e-04, obj = 1.25592868e+04, nz: 280
  30. Ttl Inner Its: 245, KKT viol = 3.78e-04, obj = 1.25592868e+04, nz: 280
  32. Ttl Inner Its: 243, KKT viol = 1.32e-04, obj = 1.25592868e+04, nz: 280
  34. Ttl Inner Its: 240, KKT viol = 9.98e-05, obj = 1.25592868e+04, nz: 280
===========================================
 Final f = 1.255929e+04 
 Final least squares fit = 5.232291e-01 
 Final KKT violation = 9.9761257e-05
 Total inner iterations = 14152
 Total execution time = 1.36 secs

CP_APR:

 Tensor size = [100 80 60], Approximation Rank = 5
 Tensor type: sparse with 10450 (2.2%) nonzeros 
 alg = 'pdnr' (damped Newton)
 stoptol = 0.0001, stoptime = 1e+06
 maxiters = 1000, maxinneriters = 10
 epsDivZero = 1e-10, epsActive = 1e-08
 mu0 = 1e-05, inexact = 1
 precompinds = 1

 Precomputing sparse index sets...done
   2. Ttl Inner Its: 324, KKT viol = 1.09e+03, obj = 5.90744136e+04, nz: 318
   4. Ttl Inner Its: 1205, KKT viol = 1.48e+03, obj = 2.03017275e+04, nz: 372
   6. Ttl Inner Its: 240, KKT viol = 3.24e+01, obj = 1.94325932e+04, nz: 326
   8. Ttl Inner Its: 487, KKT viol = 1.07e+02, obj = 1.33200711e+04, nz: 249
  10. Ttl Inner Its: 872, KKT viol = 1.90e+01, obj = 1.26266158e+04, nz: 256
  12. Ttl Inner Its: 264, KKT viol = 9.34e-01, obj = 1.25675319e+04, nz: 270
  14. Ttl Inner Its: 432, KKT viol = 3.45e-01, obj = 1.25598890e+04, nz: 276
  16. Ttl Inner Its: 273, KKT viol = 9.89e-02, obj = 1.25597954e+04, nz: 277
  18. Ttl Inner Its: 433, KKT viol = 6.45e-03, obj = 1.25597900e+04, nz: 278
  20. Ttl Inner Its: 278, KKT viol = 3.51e-03, obj = 1.25597899e+04, nz: 278
  22. Ttl Inner Its: 248, KKT viol = 1.75e-03, obj = 1.25597899e+04, nz: 278
  24. Ttl Inner Its: 244, KKT viol = 8.24e-04, obj = 1.25597899e+04, nz: 278
  26. Ttl Inner Its: 246, KKT viol = 3.94e-04, obj = 1.25597899e+04, nz: 278
  28. Ttl Inner Its: 247, KKT viol = 2.11e-04, obj = 1.25597899e+04, nz: 278
  30. Ttl Inner Its: 242, KKT viol = 1.12e-04, obj = 1.25597899e+04, nz: 278
===========================================
 Final f = 1.255979e+04 
 Final least squares fit = 5.232301e-01 
 Final KKT violation = 9.9705252e-05
 Total inner iterations = 11786
 Total execution time = 1.38 secs

CP_APR:

 Tensor size = [100 80 60], Approximation Rank = 5
 Tensor type: sparse with 10450 (2.2%) nonzeros 
 alg = 'pdnr' (damped Newton)
 stoptol = 0.0001, stoptime = 1e+06
 maxiters = 1000, maxinneriters = 10
 epsDivZero = 1e-10, epsActive = 1e-08
 mu0 = 1e-05, inexact = 1
 precompinds = 1

 Precomputing sparse index sets...done
   2. Ttl Inner Its: 578, KKT viol = 7.88e+02, obj = 3.67776143e+04, nz: 282
   4. Ttl Inner Its: 334, KKT viol = 1.48e+01, obj = 3.34715128e+04, nz: 256
   6. Ttl Inner Its: 647, KKT viol = 1.55e+02, obj = 1.53709982e+04, nz: 267
   8. Ttl Inner Its: 907, KKT viol = 2.37e+00, obj = 1.47265281e+04, nz: 271
  10. Ttl Inner Its: 490, KKT viol = 2.50e+01, obj = 1.27458113e+04, nz: 257
  12. Ttl Inner Its: 429, KKT viol = 2.23e+00, obj = 1.25642707e+04, nz: 271
  14. Ttl Inner Its: 385, KKT viol = 1.29e-01, obj = 1.25593488e+04, nz: 277
  16. Ttl Inner Its: 356, KKT viol = 3.29e-02, obj = 1.25592907e+04, nz: 279
  18. Ttl Inner Its: 319, KKT viol = 1.73e-02, obj = 1.25592877e+04, nz: 280
  20. Ttl Inner Its: 303, KKT viol = 8.70e-03, obj = 1.25592871e+04, nz: 280
  22. Ttl Inner Its: 260, KKT viol = 4.46e-03, obj = 1.25592869e+04, nz: 280
  24. Ttl Inner Its: 252, KKT viol = 2.23e-03, obj = 1.25592868e+04, nz: 280
  26. Ttl Inner Its: 252, KKT viol = 1.14e-03, obj = 1.25592868e+04, nz: 280
  28. Ttl Inner Its: 249, KKT viol = 5.76e-04, obj = 1.25592868e+04, nz: 280
  30. Ttl Inner Its: 244, KKT viol = 2.90e-04, obj = 1.25592868e+04, nz: 280
  32. Ttl Inner Its: 243, KKT viol = 1.58e-04, obj = 1.25592868e+04, nz: 280
  34. Ttl Inner Its: 240, KKT viol = 9.97e-05, obj = 1.25592868e+04, nz: 280
===========================================
 Final f = 1.255929e+04 
 Final least squares fit = 5.232289e-01 
 Final KKT violation = 9.9691480e-05
 Total inner iterations = 13453
 Total execution time = 1.28 secs

Example using the 'mu' algorithm

This example demonstrates the 'mu' algorithm. We can also set parameters specific to 'mu', like 'kappa'. Because this is faster per iteration by requires more iterations, we only print the results every 10 iterations. We run the method 5 times and keep the best solution (lowest objective value).

fprintf('--- Running CP-APR with MU ---\n');
rng('default')

best_obj_mu = inf;
for trial = 1:5
    [M_tmp,~,output_tmp] = cp_apr(X, R, 'alg', 'mu', 'printitn', 10, 'maxiters', 200, 'kappa', 50);
    if output_tmp.obj < best_obj_mu
        best_obj_mu = output_tmp.obj;
        M_mu = M_tmp;
        output_mu = output_tmp;
    end
end
% Score the solution
factor_match_score_mu = score(M_mu, M_true, 'greedy', true);

--- Running CP-APR with MU ---

CP_APR:

 Tensor size = [100 80 60], Approximation Rank = 5
 Tensor type: sparse with 10450 (2.2%) nonzeros 
 alg = 'mu' (multiplicative updates with adjustments)
 stoptol = 0.0001, stoptime = 1e+06
 maxiters = 200, maxinneriters = 10
 epsDivZero = 1e-10, kappa = 50, kappatol = 1e-10

 Iter   10: Inner Its = 30 KKT violation = 9.249377e-02, nViolations =  0, obj = 1.25598982e+04
 Iter   20: Inner Its = 30 KKT violation = 8.592690e-03, nViolations =  0, obj = 1.25597790e+04
 Iter   30: Inner Its = 24 KKT violation = 5.806821e-03, nViolations =  0, obj = 1.25597782e+04
 Iter   40: Inner Its = 15 KKT violation = 4.655408e-03, nViolations =  0, obj = 1.25597781e+04
 Iter   50: Inner Its = 12 KKT violation = 4.025659e-03, nViolations =  0, obj = 1.25597781e+04
 Iter   60: Inner Its = 12 KKT violation = 3.497964e-03, nViolations =  0, obj = 1.25597781e+04
 Iter   70: Inner Its = 12 KKT violation = 2.457578e-03, nViolations =  0, obj = 1.25597781e+04
 Iter   80: Inner Its = 12 KKT violation = 1.759166e-03, nViolations =  0, obj = 1.25597781e+04
 Iter   90: Inner Its = 12 KKT violation = 1.277045e-03, nViolations =  0, obj = 1.25597781e+04
 Iter  100: Inner Its = 12 KKT violation = 9.350392e-04, nViolations =  0, obj = 1.25597781e+04
 Iter  110: Inner Its = 12 KKT violation = 6.898427e-04, nViolations =  0, obj = 1.25597781e+04
 Iter  120: Inner Its = 12 KKT violation = 5.106160e-04, nViolations =  0, obj = 1.25597781e+04
 Iter  130: Inner Its = 12 KKT violation = 3.798073e-04, nViolations =  0, obj = 1.25597781e+04
 Iter  140: Inner Its = 12 KKT violation = 2.824650e-04, nViolations =  0, obj = 1.25597781e+04
 Iter  150: Inner Its = 12 KKT violation = 2.108602e-04, nViolations =  0, obj = 1.25597781e+04
 Iter  160: Inner Its = 12 KKT violation = 1.578435e-04, nViolations =  0, obj = 1.25597781e+04
 Iter  170: Inner Its = 12 KKT violation = 1.183998e-04, nViolations =  0, obj = 1.25597781e+04
Exiting because all subproblems reached KKT tol.
===========================================
 Final f = 1.255978e+04 
 Final least squares fit = 5.232344e-01 
 Final KKT violation = 9.9999544e-05
 Total inner iterations = 2723
 Total execution time = 1.62 secs

CP_APR:

 Tensor size = [100 80 60], Approximation Rank = 5
 Tensor type: sparse with 10450 (2.2%) nonzeros 
 alg = 'mu' (multiplicative updates with adjustments)
 stoptol = 0.0001, stoptime = 1e+06
 maxiters = 200, maxinneriters = 10
 epsDivZero = 1e-10, kappa = 50, kappatol = 1e-10

 Iter   10: Inner Its = 30 KKT violation = 4.844923e-01, nViolations =  2, obj = 1.43860744e+04
 Iter   20: Inner Its = 30 KKT violation = 1.738390e-01, nViolations =  1, obj = 1.43648752e+04
 Iter   30: Inner Its = 30 KKT violation = 7.799808e-02, nViolations =  0, obj = 1.43609810e+04
 Iter   40: Inner Its = 30 KKT violation = 1.032798e-01, nViolations =  0, obj = 1.43595585e+04
 Iter   50: Inner Its = 30 KKT violation = 4.356253e-02, nViolations =  0, obj = 1.43592219e+04
 Iter   60: Inner Its = 30 KKT violation = 2.071341e-02, nViolations =  0, obj = 1.43591517e+04
 Iter   70: Inner Its = 30 KKT violation = 7.858970e-03, nViolations =  0, obj = 1.43591337e+04
 Iter   80: Inner Its = 28 KKT violation = 7.752428e-03, nViolations =  0, obj = 1.43591298e+04
 Iter   90: Inner Its = 30 KKT violation = 7.783842e-03, nViolations =  0, obj = 1.43591274e+04
 Iter  100: Inner Its = 30 KKT violation = 7.986604e-03, nViolations =  0, obj = 1.43591236e+04
 Iter  110: Inner Its = 30 KKT violation = 8.409126e-03, nViolations =  0, obj = 1.43591173e+04
 Iter  120: Inner Its = 30 KKT violation = 8.402947e-03, nViolations =  0, obj = 1.43591128e+04
 Iter  130: Inner Its = 30 KKT violation = 3.890598e-03, nViolations =  0, obj = 1.43591073e+04
 Iter  140: Inner Its = 30 KKT violation = 3.769377e-03, nViolations =  0, obj = 1.43590991e+04
 Iter  150: Inner Its = 30 KKT violation = 3.365400e-02, nViolations =  0, obj = 1.43590918e+04
 Iter  160: Inner Its = 30 KKT violation = 4.143578e-03, nViolations =  0, obj = 1.43590671e+04
 Iter  170: Inner Its = 30 KKT violation = 3.009754e-03, nViolations =  0, obj = 1.43590386e+04
 Iter  180: Inner Its = 30 KKT violation = 4.864634e-03, nViolations =  0, obj = 1.43589935e+04
 Iter  190: Inner Its = 30 KKT violation = 1.358162e-01, nViolations =  1, obj = 1.43611969e+04
 Iter  200: Inner Its = 30 KKT violation = 3.583451e-02, nViolations =  0, obj = 1.43575841e+04
===========================================
 Final f = 1.435758e+04 
 Final least squares fit = 5.164555e-01 
 Final KKT violation = 3.5834509e-02
 Total inner iterations = 5992
 Total execution time = 3.03 secs

CP_APR:

 Tensor size = [100 80 60], Approximation Rank = 5
 Tensor type: sparse with 10450 (2.2%) nonzeros 
 alg = 'mu' (multiplicative updates with adjustments)
 stoptol = 0.0001, stoptime = 1e+06
 maxiters = 200, maxinneriters = 10
 epsDivZero = 1e-10, kappa = 50, kappatol = 1e-10

 Iter   10: Inner Its = 30 KKT violation = 4.074251e-02, nViolations =  0, obj = 1.25598024e+04
 Iter   20: Inner Its = 30 KKT violation = 7.985892e-03, nViolations =  0, obj = 1.25597901e+04
 Iter   30: Inner Its = 21 KKT violation = 5.531637e-03, nViolations =  0, obj = 1.25597899e+04
 Iter   40: Inner Its = 14 KKT violation = 4.438471e-03, nViolations =  0, obj = 1.25597899e+04
 Iter   50: Inner Its = 12 KKT violation = 3.874232e-03, nViolations =  0, obj = 1.25597899e+04
 Iter   60: Inner Its = 13 KKT violation = 3.496665e-03, nViolations =  0, obj = 1.25597899e+04
 Iter   70: Inner Its = 12 KKT violation = 2.484731e-03, nViolations =  0, obj = 1.25597899e+04
 Iter   80: Inner Its = 12 KKT violation = 1.799994e-03, nViolations =  0, obj = 1.25597899e+04
 Iter   90: Inner Its = 13 KKT violation = 1.321612e-03, nViolations =  0, obj = 1.25597899e+04
 Iter  100: Inner Its = 12 KKT violation = 9.791504e-04, nViolations =  0, obj = 1.25597899e+04
 Iter  110: Inner Its = 12 KKT violation = 7.306154e-04, nViolations =  0, obj = 1.25597899e+04
 Iter  120: Inner Its = 12 KKT violation = 5.474619e-04, nViolations =  0, obj = 1.25597899e+04
 Iter  130: Inner Its = 12 KKT violation = 4.123053e-04, nViolations =  0, obj = 1.25597899e+04
 Iter  140: Inner Its = 12 KKT violation = 3.103147e-04, nViolations =  0, obj = 1.25597899e+04
 Iter  150: Inner Its = 12 KKT violation = 2.344776e-04, nViolations =  0, obj = 1.25597899e+04
 Iter  160: Inner Its = 12 KKT violation = 1.776971e-04, nViolations =  0, obj = 1.25597899e+04
 Iter  170: Inner Its = 12 KKT violation = 1.349647e-04, nViolations =  0, obj = 1.25597899e+04
 Iter  180: Inner Its = 12 KKT violation = 1.024869e-04, nViolations =  0, obj = 1.25597899e+04
Exiting because all subproblems reached KKT tol.
===========================================
 Final f = 1.255979e+04 
 Final least squares fit = 5.232300e-01 
 Final KKT violation = 9.9944338e-05
 Total inner iterations = 2719
 Total execution time = 1.56 secs

CP_APR:

 Tensor size = [100 80 60], Approximation Rank = 5
 Tensor type: sparse with 10450 (2.2%) nonzeros 
 alg = 'mu' (multiplicative updates with adjustments)
 stoptol = 0.0001, stoptime = 1e+06
 maxiters = 200, maxinneriters = 10
 epsDivZero = 1e-10, kappa = 50, kappatol = 1e-10

 Iter   10: Inner Its = 30 KKT violation = 3.322665e-01, nViolations =  3, obj = 1.43503679e+04
 Iter   20: Inner Its = 30 KKT violation = 6.261468e-01, nViolations =  3, obj = 1.25694191e+04
 Iter   30: Inner Its = 30 KKT violation = 1.165293e-02, nViolations =  0, obj = 1.25592873e+04
 Iter   40: Inner Its = 13 KKT violation = 1.242409e-03, nViolations =  0, obj = 1.25592868e+04
 Iter   50: Inner Its = 12 KKT violation = 9.159682e-04, nViolations =  0, obj = 1.25592868e+04
 Iter   60: Inner Its = 12 KKT violation = 6.805259e-04, nViolations =  0, obj = 1.25592868e+04
 Iter   70: Inner Its = 12 KKT violation = 5.088195e-04, nViolations =  0, obj = 1.25592868e+04
 Iter   80: Inner Its = 12 KKT violation = 3.806999e-04, nViolations =  0, obj = 1.25592868e+04
 Iter   90: Inner Its = 12 KKT violation = 2.862512e-04, nViolations =  0, obj = 1.25592868e+04
 Iter  100: Inner Its = 12 KKT violation = 2.160233e-04, nViolations =  0, obj = 1.25592868e+04
 Iter  110: Inner Its = 12 KKT violation = 1.625292e-04, nViolations =  0, obj = 1.25592868e+04
 Iter  120: Inner Its = 12 KKT violation = 1.224492e-04, nViolations =  0, obj = 1.25592868e+04
Exiting because all subproblems reached KKT tol.
===========================================
 Final f = 1.255929e+04 
 Final least squares fit = 5.232290e-01 
 Final KKT violation = 9.9963935e-05
 Total inner iterations = 2203
 Total execution time = 1.23 secs

CP_APR:

 Tensor size = [100 80 60], Approximation Rank = 5
 Tensor type: sparse with 10450 (2.2%) nonzeros 
 alg = 'mu' (multiplicative updates with adjustments)
 stoptol = 0.0001, stoptime = 1e+06
 maxiters = 200, maxinneriters = 10
 epsDivZero = 1e-10, kappa = 50, kappatol = 1e-10

 Iter   10: Inner Its = 30 KKT violation = 3.324546e-01, nViolations =  1, obj = 1.43721467e+04
 Iter   20: Inner Its = 30 KKT violation = 1.254772e-01, nViolations =  1, obj = 1.43639954e+04
 Iter   30: Inner Its = 30 KKT violation = 9.974392e-02, nViolations =  1, obj = 1.43589038e+04
 Iter   40: Inner Its = 30 KKT violation = 1.314063e-01, nViolations =  1, obj = 1.43533891e+04
 Iter   50: Inner Its = 30 KKT violation = 1.138546e-01, nViolations =  1, obj = 1.43513304e+04
 Iter   60: Inner Its = 30 KKT violation = 3.344027e-02, nViolations =  0, obj = 1.43507349e+04
 Iter   70: Inner Its = 30 KKT violation = 3.036969e-02, nViolations =  0, obj = 1.43503299e+04
 Iter   80: Inner Its = 30 KKT violation = 1.267476e-01, nViolations =  2, obj = 1.43497493e+04
 Iter   90: Inner Its = 30 KKT violation = 5.061820e-01, nViolations =  1, obj = 1.43457793e+04
 Iter  100: Inner Its = 30 KKT violation = 1.366917e-01, nViolations =  3, obj = 1.43430420e+04
 Iter  110: Inner Its = 30 KKT violation = 2.003749e-02, nViolations =  0, obj = 1.43407603e+04
 Iter  120: Inner Its = 30 KKT violation = 1.892862e-02, nViolations =  0, obj = 1.43397194e+04
 Iter  130: Inner Its = 30 KKT violation = 2.069699e-02, nViolations =  0, obj = 1.43394426e+04
 Iter  140: Inner Its = 30 KKT violation = 1.989947e-02, nViolations =  0, obj = 1.43393698e+04
 Iter  150: Inner Its = 30 KKT violation = 1.591972e-02, nViolations =  0, obj = 1.43393514e+04
 Iter  160: Inner Its = 25 KKT violation = 1.597734e-02, nViolations =  0, obj = 1.43393468e+04
 Iter  170: Inner Its = 23 KKT violation = 1.011655e-02, nViolations =  0, obj = 1.43393454e+04
 Iter  180: Inner Its = 22 KKT violation = 6.328913e-03, nViolations =  0, obj = 1.43393450e+04
 Iter  190: Inner Its = 21 KKT violation = 4.910786e-03, nViolations =  0, obj = 1.43393448e+04
 Iter  200: Inner Its = 13 KKT violation = 4.885278e-03, nViolations =  0, obj = 1.43393447e+04
===========================================
 Final f = 1.433934e+04 
 Final least squares fit = 5.154573e-01 
 Final KKT violation = 4.8852779e-03
 Total inner iterations = 5629
 Total execution time = 3.58 secs

Comparing results

We can see that all methods can find a reasonable solution, though convergence speed and final accuracy might differ. The 'pqnr' and 'pdnr' methods are generally more sophisticated and may converge to a better solution or faster in terms of outer iterations, while 'mu' iterations are typically cheaper.

For this particular problem and random initialization:

fprintf('Factor Match Score (PQNR): %.4f\n', factor_match_score_pqnr);
fprintf('Factor Match Score (PDNR): %.4f\n', factor_match_score_pdnr);
fprintf('Factor Match Score (MU):   %.4f\n', factor_match_score_mu);

Factor Match Score (PQNR): 0.9744
Factor Match Score (PDNR): 0.9744
Factor Match Score (MU):   0.9744

Visualize the results

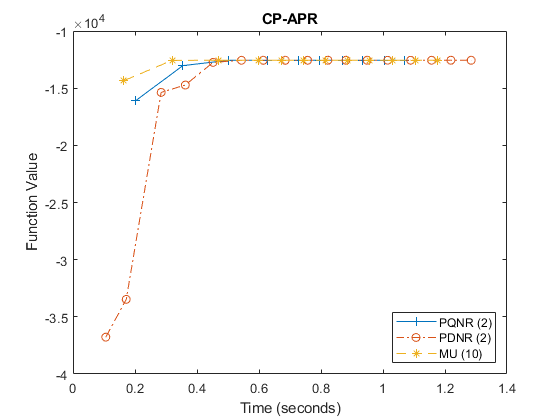
The function values are only computed when printing the output to the screen. The legend indicates the method and, in parentheses, how frequently the objective value was recorded.

figure(1); clf;
tf = ~isnan(output_pqnr.fnVals);
plot(output_pqnr.times(tf), 1-output_pqnr.fnVals(tf),'-+','DisplayName','PQNR (2)');

hold on;
tf = ~isnan(output_pdnr.fnVals);
plot(output_pdnr.times(tf), 1-output_pdnr.fnVals(tf),'-.o', 'DisplayName','PDNR (2)');

tf = ~isnan(output_mu.fnVals);
plot(output_mu.times(tf), 1-output_mu.fnVals(tf),'--*', 'DisplayName','MU (10)');
hold off;

title('CP-APR');
xlabel('Time (seconds)');
ylabel('Function Value');
legend('Location','SouthEast')