Symmetric Tensors
A symmetric tensor is a tensor that is invariant under all permutations of its modes. Because many of the elements of a symmetric tensor are guaranteed to be equal, we can simplify the storage requirements by only storing the unique values of the symmetric tensor. There are 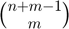 such values for an m-way tensor of dimension n. The symtensor class is designed to take advantage of this symmetric structure by only storing the unique values of the tensor.
such values for an m-way tensor of dimension n. The symtensor class is designed to take advantage of this symmetric structure by only storing the unique values of the tensor.
Contents
- Definition of a symmetric tensor
- Creating a symtensor from a symmetric tensor
- Unique entries of a tensor
- Creating a symtensor from a nonsymmetric tensor
- Create an all ones symtensor
- Create a random symtensor
- Using a generating function to populate a symmetric tensor
- Use ndims and size to get the size of a symmetric tensor
- Use full to convert a symmetric tensor to a multidimensional array
- Subscripted reference of a symmetric tensor
- Subscripted assignment
- Basic operations (plus, minus, and, or, etc.) on a symmetric tensor
- Using symtenfun for elementwise operations on one or more symmetric tensors
Definition of a symmetric tensor
A symmetric tensor is invariant under any permutation of the indices. Here is a small example. The issymmetric function checks symmetry of a dense tensor.
T(:,:,1) = [1 2; 2 3]; T(:,:,2)= [2 3; 3 6]; T = tensor(T) issymmetric(T)
T is a tensor of size 2 x 2 x 2 T(:,:,1) = 1 2 2 3 T(:,:,2) = 2 3 3 6 ans = logical 1
Creating a symtensor from a symmetric tensor
We can construct a symtensor object from a symmetric tensor. This object only stores the unique entries of the tensor. For the 2 x 2 x 2 tensor, this means there are only four unique entries. Everything else comes from permuting the indices of those four entries.
S = symtensor(T)
S is a symmetric tensor with 3 modes of dimension 2 (1,1,1) 1 (1,1,2) 2 (1,2,2) 3 (2,2,2) 6
Unique entries of a tensor
Note from TGK: This needs to be added. It should have some discussion of all the return values from indices. What is a monomial description, etc.
[I,C,W,Q] = indices(S)
I =
1 1 1
1 1 2
1 2 2
2 2 2
C =
3 0
2 1
1 2
0 3
W =
1
3
3
1
Q =
4
Creating a symtensor from a nonsymmetric tensor
A symmetric tensors can be created from the symmetrization of nonsymmetric tensor so long as it is the same size in every mode. If the input is not symmetric, it is symmetrized by creating an average of elements in the same permutation class. For instance, this example starts with a nonsymmetric tensor and symmetrizes it:
T2 = tensor([1:8],[2 2 2]) S2 = symtensor(T2)
T2 is a tensor of size 2 x 2 x 2 T2(:,:,1) = 1 3 2 4 T2(:,:,2) = 5 7 6 8 S2 is a symmetric tensor with 3 modes of dimension 2 (1,1,1) 1.0000 (1,1,2) 3.3333 (1,2,2) 5.6667 (2,2,2) 8.0000
Converting the symtensor back to a generic tensor is equivalent to running symmetrize on the original tensor. In the following example, the full command converts a symtensor to a tensor.
full(S2) symmetrize(T2)
ans is a tensor of size 2 x 2 x 2 ans(:,:,1) = 1.0000 3.3333 3.3333 5.6667 ans(:,:,2) = 3.3333 5.6667 5.6667 8.0000 ans is a tensor of size 2 x 2 x 2 ans(:,:,1) = 1.0000 3.3333 3.3333 5.6667 ans(:,:,2) = 3.3333 5.6667 5.6667 8.0000
Create an all ones symtensor
The first argument is the generating function, the second argument is the number of modes, and the third argument is the size of each mode.
S3 = symtensor(@ones, 3, 2)
S3 is a symmetric tensor with 3 modes of dimension 2 (1,1,1) 1 (1,1,2) 1 (1,2,2) 1 (2,2,2) 1
Create a random symtensor
rng('default'); %<- Setting random seed for reproducibility of this script S4 = symtensor(@randn, 3, 2)
S4 is a symmetric tensor with 3 modes of dimension 2 (1,1,1) 0.5377 (1,1,2) 1.8339 (1,2,2) -2.2588 (2,2,2) 0.8622
Using a generating function to populate a symmetric tensor
In general, a symmetric tensor can also have its entries created by any generating function. This is done by passing a function handle, the number of modes, and the dimension. The function is expected to take a two-dimension size as input and return a matrix of that shape. In fact, the second argument to the function will always be 1.
% For example, we can also declare a binary symmetric tensor as follows:
S5 = symtensor(@(x,y) double(rand(x,y)>.25), 3, 3)
S5 is a symmetric tensor with 3 modes of dimension 3 (1,1,1) 1 (1,1,2) 0 (1,1,3) 1 (1,2,2) 1 (1,2,3) 1 (1,3,3) 1 (2,2,2) 0 (2,2,3) 1 (2,3,3) 1 (3,3,3) 1
Use ndims and size to get the size of a symmetric tensor
ndims(S) %<-- Number of modes of the symmetric tensor
ans =
3
size(S) %<-- Size of a symmetric tensor
ans =
2 2 2
Use full to convert a symmetric tensor to a multidimensional array
full(S) %<-- Converts from a symmetric tensor to a tensor
ans is a tensor of size 2 x 2 x 2 ans(:,:,1) = 1 2 2 3 ans(:,:,2) = 2 3 3 6
Subscripted reference of a symmetric tensor
Subindex notation extracts the tensor value.
S(1,2,2)
S(2,1,2) %<-- Equal to above, by symmetry
ans =
3
ans =
3
This works the same as applying it to the full tensor.
T(1,2,2) T(2,1,2)
ans =
3
ans =
3
Multiple indices can be queried by combining these indices into the rows of a matrix. Consider the following example, which returns a vector consisting of the values of S at indices indicated by the rows of the input matrix.
S([1 2 1; 2 1 2])
ans =
2
3
Single indices are interpretted as an index into the unique value array, which is stored with respect to increasing indices. This is very different than using linear indexing on the full tensor.
S(3) %<- Third unique entry corresponding to (1,2,2) S(4) %<- Fourth unique entry, corresponding to (2,2,2) T(3) %<- Third entry in the tensor, i.e., (1,2,1) = (1,1,2) T(4) %<- Fourth entry in the tensor, i.e., (2,2,1) = (1,2,2)
ans =
3
ans =
6
ans =
2
ans =
3
Mulitple entries can be obtained at once as well.
S([3:4]')
ans =
3
6
Subscripted assignment
Symmetric tensors also support subscripted assignment. Either linear or subindex notation is valid. Multiple values can be assigned the same quantity, but assigning a subset of a symmetric tensor from a multidimensional arrays, tensor, or symtensor is not allowed.
S5(1) = 7 %<-- Linear indexing S5(2,1,2) = 6 %<-- Subindex indexing
S5 is a symmetric tensor with 3 modes of dimension 3 (1,1,1) 7 (1,1,2) 0 (1,1,3) 1 (1,2,2) 1 (1,2,3) 1 (1,3,3) 1 (2,2,2) 0 (2,2,3) 1 (2,3,3) 1 (3,3,3) 1 S5 is a symmetric tensor with 3 modes of dimension 3 (1,1,1) 7 (1,1,2) 0 (1,1,3) 1 (1,2,2) 6 (1,2,3) 1 (1,3,3) 1 (2,2,2) 0 (2,2,3) 1 (2,3,3) 1 (3,3,3) 1
Symmetric tensors do not support enlargement with the assignment operator, so assigning a value to an index other than those which have already been declared produces an error.
Basic operations (plus, minus, and, or, etc.) on a symmetric tensor
The tensor object supports many basic operations, illustrated here.
A = symtensor(@(x,y) rand(x,y)>.5, 3, 2) B = symtensor(@(x,y) rand(x,y)>.5, 3, 2)
A is a symmetric tensor with 3 modes of dimension 2 (1,1,1) 1 (1,1,2) 0 (1,2,2) 0 (2,2,2) 1 B is a symmetric tensor with 3 modes of dimension 2 (1,1,1) 1 (1,1,2) 1 (1,2,2) 1 (2,2,2) 0
A==B %<-- Calls eq.
ans is a symmetric tensor with 3 modes of dimension 2 (1,1,1) 1 (1,1,2) 0 (1,2,2) 0 (2,2,2) 0
A<B %<-- Calls lt.
ans is a symmetric tensor with 3 modes of dimension 2 (1,1,1) 0 (1,1,2) 1 (1,2,2) 1 (2,2,2) 0
A.*B %<-- Calls times. (elementwise multiply)
ans is a symmetric tensor with 3 modes of dimension 2 (1,1,1) 1 (1,1,2) 0 (1,2,2) 0 (2,2,2) 0
5*A %<-- Calls mtimes. (scalar multiply)
ans is a symmetric tensor with 3 modes of dimension 2 (1,1,1) 5 (1,1,2) 0 (1,2,2) 0 (2,2,2) 5
The symtensor class supports the following additional MATLABbinary operations: and, or, xor, neq, gt, ge, le, plus, minus, power, ldivide, and rdivide. Supported unary operations include: not, uplus, uminus.
Using symtenfun for elementwise operations on one or more symmetric tensors
The function symtenfun applies a function to a number of symmetric symtensors. This function mirrors the capability of tenfun for tensors.
tenfun(@min, S, S2, S+1) %<-- Symtensor formed from elementwise minimization
ans is a symmetric tensor with 3 modes of dimension 2 (1,1,1) 1 (1,1,2) 2 (1,2,2) 3 (2,2,2) 6
tenfun(@(x)(x-1.5),S) %<-- Subtract 1.5 from each element of B
ans is a symmetric tensor with 3 modes of dimension 2 (1,1,1) -0.5000 (1,1,2) 0.5000 (1,2,2) 1.5000 (2,2,2) 4.5000
