Alternating least squares for CANDECOMP/PARAFAC (CP) Decomposition

>> Tensor Toolbox >> CP Decompositions >> CP-ALS

The function cp_als computes an estimate of the best rank-R CP model of a tensor X using the well-known alternating least-squares algorithm (see, e.g., Kolda and Bader, SIAM Review, 2009, for more information). The input X can be almost any type of tensor inclusing a tensor, sptensor, ktensor, or ttensor. The output CP model is a ktensor.

Contents

Load some data

We use the well-known amino acids data set from Andersson and Bro. It contains fluorescence measurements of 5 samples containing 3 amino acids: Tryptophan, Tyrosine, and Phenylalanine.Each amino acid corresponds to a rank-one component. The tensor is of size 5 x 51 x 201 from 5 samples, 51 excitations, and 201 emissions. Further details can be found here: http://www.models.life.ku.dk/Amino_Acid_fluo. Please cite the following paper for this data: Rasmus Bro, PARAFAC: Tutorial and applications, Chemometrics and Intelligent Laboratory Systems, 1997, 38, 149-171. This dataset can be found in the doc directory.

load aminoacids

Basic call to the method, specifying the data tensor and its rank

This uses a random initial guess. At each iteration, it reports the 'fit' which is defined as 1-(norm(X-M)/norm(X)) and is loosely the proportion of the data described by the CP model, i.e., a fit of 1 is perfect.

rng('default') %<- Setting random seed for reproducibility of this script
M1 = cp_als(X,3); %<- Call the method

CP_ALS (CP Alternating Least Squares):

 Tensor size: [5 201 61]
 Tensor type: tensor
 R = 3, maxiters = 50, tol = 1.000000e-04
 dimorder = [1 2 3]
 init = random

 Iter  1: f = 5.191033e-01 f-delta = 5.2e-01
 Iter  2: f = 6.617871e-01 f-delta = 1.4e-01
 Iter  3: f = 7.615352e-01 f-delta = 1.0e-01
 Iter  4: f = 8.286421e-01 f-delta = 6.7e-02
 Iter  5: f = 8.813646e-01 f-delta = 5.3e-02
 Iter  6: f = 9.349259e-01 f-delta = 5.4e-02
 Iter  7: f = 9.592629e-01 f-delta = 2.4e-02
 Iter  8: f = 9.671789e-01 f-delta = 7.9e-03
 Iter  9: f = 9.702331e-01 f-delta = 3.1e-03
 Iter 10: f = 9.715826e-01 f-delta = 1.3e-03
 Iter 11: f = 9.722850e-01 f-delta = 7.0e-04
 Iter 12: f = 9.727265e-01 f-delta = 4.4e-04
 Iter 13: f = 9.730506e-01 f-delta = 3.2e-04
 Iter 14: f = 9.733119e-01 f-delta = 2.6e-04
 Iter 15: f = 9.735326e-01 f-delta = 2.2e-04
 Iter 16: f = 9.737227e-01 f-delta = 1.9e-04
 Iter 17: f = 9.738876e-01 f-delta = 1.6e-04
 Iter 18: f = 9.740309e-01 f-delta = 1.4e-04
 Iter 19: f = 9.741554e-01 f-delta = 1.2e-04
 Iter 20: f = 9.742635e-01 f-delta = 1.1e-04
 Iter 21: f = 9.743572e-01 f-delta = 9.4e-05
 Final f = 9.743572e-01 

We typically can achieve a final fit of f = 0.97. The method stops when the change in the fit becomes less than the specified tolerance, which defaults to 1-e4.

Visualize the results

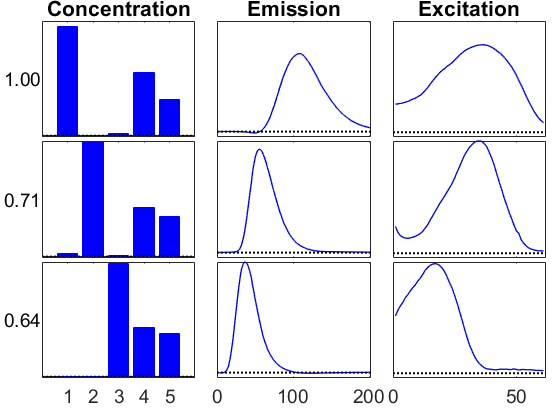
Use the ktensor/viz function to visualize the results.

vizopts = {'PlotCommands',{'bar','line','line'},...
    'ModeTitles',{'Concentration','Emission','Excitation'},...
    'BottomSpace',0.10,'HorzSpace',0.04,'Normalize',0};
info1 = viz(M1,'Figure',1,vizopts{:});

Run again with a different initial guess, output the initial guess.

This time we have two outputs. The first output is the solution as a ktensor. The second output is a cell array containing the initial guess. Since the first mode is not needed, it is omitted from the cell array.

rng(7) % Reproducibility
[M2bad,U2] = cp_als(X,3);

CP_ALS (CP Alternating Least Squares):

 Tensor size: [5 201 61]
 Tensor type: tensor
 R = 3, maxiters = 50, tol = 1.000000e-04
 dimorder = [1 2 3]
 init = random

 Iter  1: f = 4.656532e-01 f-delta = 4.7e-01
 Iter  2: f = 6.849381e-01 f-delta = 2.2e-01
 Iter  3: f = 7.873635e-01 f-delta = 1.0e-01
 Iter  4: f = 9.084899e-01 f-delta = 1.2e-01
 Iter  5: f = 9.477155e-01 f-delta = 3.9e-02
 Iter  6: f = 9.633209e-01 f-delta = 1.6e-02
 Iter  7: f = 9.692590e-01 f-delta = 5.9e-03
 Iter  8: f = 9.715954e-01 f-delta = 2.3e-03
 Iter  9: f = 9.726257e-01 f-delta = 1.0e-03
 Iter 10: f = 9.731706e-01 f-delta = 5.4e-04
 Iter 11: f = 9.735185e-01 f-delta = 3.5e-04
 Iter 12: f = 9.737732e-01 f-delta = 2.5e-04
 Iter 13: f = 9.739743e-01 f-delta = 2.0e-04
 Iter 14: f = 9.741386e-01 f-delta = 1.6e-04
 Iter 15: f = 9.742746e-01 f-delta = 1.4e-04
 Iter 16: f = 9.743880e-01 f-delta = 1.1e-04
 Iter 17: f = 9.744824e-01 f-delta = 9.4e-05
 Final f = 9.744824e-01 

Increase the maximium number of iterations

Note that the previous run kicked out at only 50 iterations before reaching the specified convegence tolerance. Let's increase the maximum number of iterations and try again, using the same initial guess.

M2 = cp_als(X,3,'maxiters',100,'init',U2);

CP_ALS (CP Alternating Least Squares):

 Tensor size: [5 201 61]
 Tensor type: tensor
 R = 3, maxiters = 100, tol = 1.000000e-04
 dimorder = [1 2 3]
 init = user-specified

 Iter  1: f = 4.656532e-01 f-delta = 4.7e-01
 Iter  2: f = 6.849381e-01 f-delta = 2.2e-01
 Iter  3: f = 7.873635e-01 f-delta = 1.0e-01
 Iter  4: f = 9.084899e-01 f-delta = 1.2e-01
 Iter  5: f = 9.477155e-01 f-delta = 3.9e-02
 Iter  6: f = 9.633209e-01 f-delta = 1.6e-02
 Iter  7: f = 9.692590e-01 f-delta = 5.9e-03
 Iter  8: f = 9.715954e-01 f-delta = 2.3e-03
 Iter  9: f = 9.726257e-01 f-delta = 1.0e-03
 Iter 10: f = 9.731706e-01 f-delta = 5.4e-04
 Iter 11: f = 9.735185e-01 f-delta = 3.5e-04
 Iter 12: f = 9.737732e-01 f-delta = 2.5e-04
 Iter 13: f = 9.739743e-01 f-delta = 2.0e-04
 Iter 14: f = 9.741386e-01 f-delta = 1.6e-04
 Iter 15: f = 9.742746e-01 f-delta = 1.4e-04
 Iter 16: f = 9.743880e-01 f-delta = 1.1e-04
 Iter 17: f = 9.744824e-01 f-delta = 9.4e-05
 Final f = 9.744824e-01 

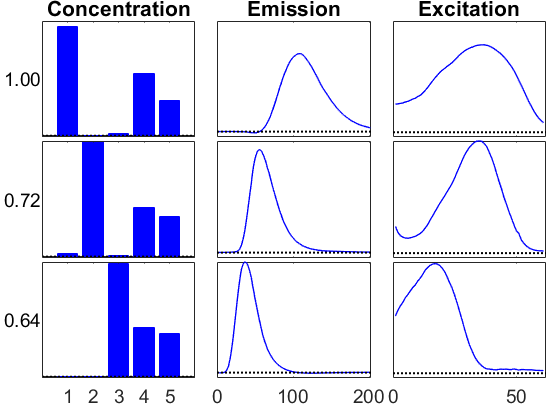
This solution looks more or less the same as the previous one.

info2 = viz(M2,'Figure',2,vizopts{:});

Compare the two solutions

Use the ktensor/score function to compare the two solutions. A score of 1 indicates a perfect match. These are not exactly the same, but they are pretty close.

score(M1,M2)

ans =

    0.9882

Rerun with same initial guess

Using the same initial guess (and all other parameters) gives the exact same solution (even without resetting the random number generator).

M2alt = cp_als(X,3,'maxiters',100,'init',U2);
score(M2, M2alt) %<- Score of 1 indicates the same solution

CP_ALS (CP Alternating Least Squares):

 Tensor size: [5 201 61]
 Tensor type: tensor
 R = 3, maxiters = 100, tol = 1.000000e-04
 dimorder = [1 2 3]
 init = user-specified

 Iter  1: f = 4.656532e-01 f-delta = 4.7e-01
 Iter  2: f = 6.849381e-01 f-delta = 2.2e-01
 Iter  3: f = 7.873635e-01 f-delta = 1.0e-01
 Iter  4: f = 9.084899e-01 f-delta = 1.2e-01
 Iter  5: f = 9.477155e-01 f-delta = 3.9e-02
 Iter  6: f = 9.633209e-01 f-delta = 1.6e-02
 Iter  7: f = 9.692590e-01 f-delta = 5.9e-03
 Iter  8: f = 9.715954e-01 f-delta = 2.3e-03
 Iter  9: f = 9.726257e-01 f-delta = 1.0e-03
 Iter 10: f = 9.731706e-01 f-delta = 5.4e-04
 Iter 11: f = 9.735185e-01 f-delta = 3.5e-04
 Iter 12: f = 9.737732e-01 f-delta = 2.5e-04
 Iter 13: f = 9.739743e-01 f-delta = 2.0e-04
 Iter 14: f = 9.741386e-01 f-delta = 1.6e-04
 Iter 15: f = 9.742746e-01 f-delta = 1.4e-04
 Iter 16: f = 9.743880e-01 f-delta = 1.1e-04
 Iter 17: f = 9.744824e-01 f-delta = 9.4e-05
 Final f = 9.744824e-01 

ans =

     1

Changing the output frequency

Using the 'printitn' option to change the output frequency.

M2alt2 = cp_als(X,3,'maxiters',100,'init',U2,'printitn',10);

CP_ALS (CP Alternating Least Squares):

 Tensor size: [5 201 61]
 Tensor type: tensor
 R = 3, maxiters = 100, tol = 1.000000e-04
 dimorder = [1 2 3]
 init = user-specified

 Iter 10: f = 9.731706e-01 f-delta = 5.4e-04
 Iter 17: f = 9.744824e-01 f-delta = 9.4e-05
 Final f = 9.744824e-01 

Suppress all output

Set 'printitn' to zero to suppress all output.

M2alt3 = cp_als(X,3,'maxiters',100,'init',U2,'printitn',0); % <-No output

Use HOSVD initial guess

Use the 'nvecs' option to use the leading mode-n singular vectors as the initial guess.

M3 = cp_als(X,3,'init','nvecs','printitn',10);

CP_ALS (CP Alternating Least Squares):

 Tensor size: [5 201 61]
 Tensor type: tensor
 R = 3, maxiters = 50, tol = 1.000000e-04
 dimorder = [1 2 3]
 init = nvecs

 Iter 10: f = 9.334888e-01 f-delta = 3.5e-03
 Iter 20: f = 9.604549e-01 f-delta = 1.9e-03
 Iter 30: f = 9.712518e-01 f-delta = 5.8e-04
 Iter 40: f = 9.741285e-01 f-delta = 1.4e-04
 Iter 43: f = 9.744312e-01 f-delta = 8.6e-05
 Final f = 9.744312e-01 

Compare to the first solution using score, and see they are nearly the same because the score is close to 1.

score(M1,M3)

ans =

    0.9832

Change the order of the dimensions in CP

rng('default') % Reproducibility
[M4,~,info4] = cp_als(X,3,'dimorder',[2 3 1],'init','nvecs','printitn',10);
score(M1,M4)

CP_ALS (CP Alternating Least Squares):

 Tensor size: [5 201 61]
 Tensor type: tensor
 R = 3, maxiters = 50, tol = 1.000000e-04
 dimorder = [2 3 1]
 init = nvecs

 Iter 10: f = 9.449957e-01 f-delta = 3.1e-03
 Iter 20: f = 9.657394e-01 f-delta = 1.3e-03
 Iter 30: f = 9.727566e-01 f-delta = 3.5e-04
 Iter 39: f = 9.743928e-01 f-delta = 9.2e-05
 Final f = 9.743928e-01 

ans =

    0.9829

In the last example, we also collected the third output argument which has some extra information in it. The field info.iters has the total number of iterations. The field info.params has the information used to run the method. Unless the initialization method is 'random', passing the parameters back to the method will yield the exact same results.

M4alt = cp_als(X,3,info4.params);
isequal(M4, M4alt) %<- Check that the solutions are identical

CP_ALS (CP Alternating Least Squares):

 Tensor size: [5 201 61]
 Tensor type: tensor
 R = 3, maxiters = 50, tol = 1.000000e-04
 dimorder = [2 3 1]
 init = nvecs

 Iter 10: f = 9.449957e-01 f-delta = 3.1e-03
 Iter 20: f = 9.657394e-01 f-delta = 1.3e-03
 Iter 30: f = 9.727566e-01 f-delta = 3.5e-04
 Iter 39: f = 9.743928e-01 f-delta = 9.2e-05
 Final f = 9.743928e-01 

ans =

  logical

   1

Change the tolerance

It's also possible to loosen or tighten the tolerance on the change in the fit. You may need to increase the number of iterations for it to converge.

rng('default') % Reproducibility
M5 = cp_als(X,3,'init','nvecs','tol',1e-6,'maxiters',1000,'printitn',10);

CP_ALS (CP Alternating Least Squares):

 Tensor size: [5 201 61]
 Tensor type: tensor
 R = 3, maxiters = 1000, tol = 1.000000e-06
 dimorder = [1 2 3]
 init = nvecs

 Iter 10: f = 9.334888e-01 f-delta = 3.5e-03
 Iter 20: f = 9.604549e-01 f-delta = 1.9e-03
 Iter 30: f = 9.712518e-01 f-delta = 5.8e-04
 Iter 40: f = 9.741285e-01 f-delta = 1.4e-04
 Iter 50: f = 9.747733e-01 f-delta = 2.9e-05
 Iter 60: f = 9.749128e-01 f-delta = 6.4e-06
 Iter 70: f = 9.749430e-01 f-delta = 1.4e-06
 Iter 73: f = 9.749461e-01 f-delta = 8.8e-07
 Final f = 9.749461e-01 

Control sign ambiguity of factor matrices

The default behavior of cp_als is to make a call to fixsigns to fix the sign ambiguity of the factor matrices. You can turn off this behavior by passing the 'fixsigns' parameter value of false when calling cp_als.

Y = ktensor([1;1], {[1, 1; 1, -10],[1, 1; 1, -10]});
M = cp_als(Y, 2, 'printitn', 0, 'init', Y) % <-default behavior, fixsigns called
M = cp_als(Y, 2, 'printitn', 0, 'init', Y, 'fixsigns', false) % <-fixsigns not called

M is a ktensor of size 2 x 2
	M.lambda = 
		  101.0000    2.0000
	M.U{1} = 
		   -0.0995    0.7071
		    0.9950    0.7071
	M.U{2} = 
		   -0.0995    0.7071
		    0.9950    0.7071
M is a ktensor of size 2 x 2
	M.lambda = 
		  101.0000    2.0000
	M.U{1} = 
		    0.0995    0.7071
		   -0.9950    0.7071
	M.U{2} = 
		    0.0995    0.7071
		   -0.9950    0.7071

Time and Convergence Trace

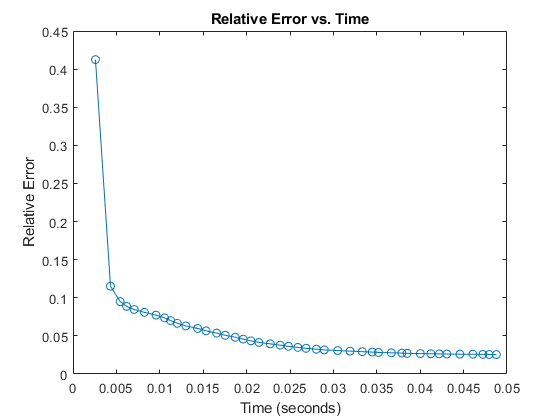
You can also time the method by passing the 'trace' parameter value of true. This will return the time it took to run the method in the output structure as well as the fit (relative error is one minus the fit) at each iteration.

rng('default') % Reproducibility
[M6, ~, output6] = cp_als(X,3,'init','nvecs','trace',true,'printitn',10);
figure(3); clf;
plot(output6.time_trace, 1-output6.fit_trace,'-o');
title('Relative Error vs. Time');
xlabel('Time (seconds)');
ylabel('Relative Error');

CP_ALS (CP Alternating Least Squares):

 Tensor size: [5 201 61]
 Tensor type: tensor
 R = 3, maxiters = 50, tol = 1.000000e-04
 dimorder = [1 2 3]
 init = nvecs

 Iter 10: f = 9.334888e-01 f-delta = 3.5e-03
 Iter 20: f = 9.604549e-01 f-delta = 1.9e-03
 Iter 30: f = 9.712518e-01 f-delta = 5.8e-04
 Iter 40: f = 9.741285e-01 f-delta = 1.4e-04
 Iter 43: f = 9.744312e-01 f-delta = 8.6e-05
 Final f = 9.744312e-01 

Recommendations

Tensor Toolbox for MATLAB: www.tensortoolbox.org.