Orthogonalized Alternating least squares for CANDECOMP/PARAFAC (CP) Decomposition

>> Tensor Toolbox >> CP Decompositions >> Orth-ALS

The function cp_orth_als is a modification of the standard CP-ALS method by orthogonalizing the factor matrices before each iteration. The parameter 'stop_orth' can be used to stop the orthogonalization after a fixed number of iterations.

IMPORTANT NOTE: This method may not converge and may not produce orthgonal factors. It is a specialized method for a specific purpose.

Orthogonalized ALS (Orth-ALS) is a modification of the ALS approach that provably recovers the true factors with random initialization under standard incoherence assumptions on the factors of the tensor. This algorithm is a modification of the ALS algorithm to "orthogonalize" the estimates of the factors before each iteration. Intuitively, this periodic orthogonalization prevents multiple recovered factors from "chasing after" the same true factors, potentially allowing for the avoidance of local optima and more rapid convergence to the true factors.

Refer to the paper for more details:

V. Sharan and G. Valiant. Orthogonalized ALS: A theoretically principled tensor decomposition algorithm for practical use. In International Conference on Machine Learning, 2017.

Recommendation
Example performance on noise-free problem with nearly orthogonal matrices
Example performance on Amino Acids test problem.

Recommendation

In practice, we have observed that it is sometimes useful to orthogonalize the factor estimates for a few iterations, and then continue with standard ALS. This is true when factors have a high correlation with each other, such as in low-dimensional settings. Our advice to practitioners would be to tune the number of steps for which orthogonalization takes place to get the best results.

Example performance on noise-free problem with nearly orthogonal matrices

Standard normal factor matrices with 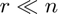$r \ll n$ are incoherent and meet the conditions of the theory. We see that cp_orth_als gets a better fit than cp_als and is faster than cp_opt.

% Setting up the problem
rng('default')
n = 100; r = 10;
U = cell(3,1);
for k = 1:3
    U{k} = (1/sqrt(n))*randn(n,r);
end
Mtrue = ktensor(U);
Xeasy = full(Mtrue);

Running cp_orth_als yields the desired solution.

rng('default')
tic
M = cp_orth_als(Xeasy,r);
toc

CP_OrthALS:
Orthogonalized, Iter  1: f = 1.572768e-01 f-delta = 1.6e-01
Orthogonalized, Iter  2: f = 5.661576e-01 f-delta = 4.1e-01
Orthogonalized, Iter  3: f = 9.558123e-01 f-delta = 3.9e-01
Orthogonalized, Iter  4: f = 9.763308e-01 f-delta = 2.1e-02
Orthogonalized, Iter  5: f = 9.766295e-01 f-delta = 3.0e-04
Orthogonalized, Iter  6: f = 9.766342e-01 f-delta = 4.8e-06
 Final f = 9.766342e-01 
Elapsed time is 0.053774 seconds.

Running cp_als does not yield the desired solution.

rng('default')
tic
M = cp_als(Xeasy,r);
toc

CP_ALS:
 Iter  1: f = 1.572768e-01 f-delta = 1.6e-01
 Iter  2: f = 3.383298e-01 f-delta = 1.8e-01
 Iter  3: f = 6.117054e-01 f-delta = 2.7e-01
 Iter  4: f = 7.610412e-01 f-delta = 1.5e-01
 Iter  5: f = 7.736808e-01 f-delta = 1.3e-02
 Iter  6: f = 7.738682e-01 f-delta = 1.9e-04
 Iter  7: f = 7.738687e-01 f-delta = 4.4e-07
 Final f = 7.738687e-01 
Elapsed time is 0.052601 seconds.

Running cp_orth_als for just 2 iterations "fixes" cp_als and even yields an improved fit compared to the default of orthogonalizing at every iteration.

rng('default')
tic
M = cp_orth_als(Xeasy,r,'stop_orth',2);
toc

CP_OrthALS:
Orthogonalized, Iter  1: f = 1.572768e-01 f-delta = 1.6e-01
Orthogonalized, Iter  2: f = 5.661576e-01 f-delta = 4.1e-01
Not Orthogonalized, Iter  3: f = 8.790981e-01 f-delta = 3.1e-01
Not Orthogonalized, Iter  4: f = 9.736677e-01 f-delta = 9.5e-02
Not Orthogonalized, Iter  5: f = 9.985976e-01 f-delta = 2.5e-02
Not Orthogonalized, Iter  6: f = 9.999653e-01 f-delta = 1.4e-03
Not Orthogonalized, Iter  7: f = 9.999978e-01 f-delta = 3.3e-05
 Final f = 9.999978e-01 
Elapsed time is 0.057350 seconds.

Example performance on Amino Acids test problem.

We use the well-known amino acids data set from Andersson and Bro. It contains fluorescence measurements of 5 samples containing 3 amino acids: Tryptophan, Tyrosine, and Phenylalanine.Each amino acid corresponds to a rank-one component. The tensor is of size 5 x 51 x 201 from 5 samples, 51 excitations, and 201 emissions. Further details can be found here: http://www.models.life.ku.dk/Amino_Acid_fluo. Please cite the following paper for this data: Rasmus Bro, PARAFAC: Tutorial and applications, Chemometrics and Intelligent Laboratory Systems, 1997, 38, 149-171. This dataset can be found in the doc directory.

load aminoacids

We know that cp_als can solve this problem, and the final "fit" of 0.97 is evidence of this.

rng('default')
tic
M = cp_als(X,3);
toc

CP_ALS:
 Iter  1: f = 5.757392e-01 f-delta = 5.8e-01
 Iter  2: f = 6.397722e-01 f-delta = 6.4e-02
 Iter  3: f = 6.475932e-01 f-delta = 7.8e-03
 Iter  4: f = 6.569483e-01 f-delta = 9.4e-03
 Iter  5: f = 6.784483e-01 f-delta = 2.1e-02
 Iter  6: f = 7.272329e-01 f-delta = 4.9e-02
 Iter  7: f = 7.743007e-01 f-delta = 4.7e-02
 Iter  8: f = 8.109037e-01 f-delta = 3.7e-02
 Iter  9: f = 8.574394e-01 f-delta = 4.7e-02
 Iter 10: f = 9.072207e-01 f-delta = 5.0e-02
 Iter 11: f = 9.370083e-01 f-delta = 3.0e-02
 Iter 12: f = 9.516441e-01 f-delta = 1.5e-02
 Iter 13: f = 9.595934e-01 f-delta = 7.9e-03
 Iter 14: f = 9.640126e-01 f-delta = 4.4e-03
 Iter 15: f = 9.665412e-01 f-delta = 2.5e-03
 Iter 16: f = 9.681171e-01 f-delta = 1.6e-03
 Iter 17: f = 9.692201e-01 f-delta = 1.1e-03
 Iter 18: f = 9.700730e-01 f-delta = 8.5e-04
 Iter 19: f = 9.707752e-01 f-delta = 7.0e-04
 Iter 20: f = 9.713716e-01 f-delta = 6.0e-04
 Iter 21: f = 9.718846e-01 f-delta = 5.1e-04
 Iter 22: f = 9.723272e-01 f-delta = 4.4e-04
 Iter 23: f = 9.727090e-01 f-delta = 3.8e-04
 Iter 24: f = 9.730376e-01 f-delta = 3.3e-04
 Iter 25: f = 9.733198e-01 f-delta = 2.8e-04
 Iter 26: f = 9.735616e-01 f-delta = 2.4e-04
 Iter 27: f = 9.737684e-01 f-delta = 2.1e-04
 Iter 28: f = 9.739449e-01 f-delta = 1.8e-04
 Iter 29: f = 9.740954e-01 f-delta = 1.5e-04
 Iter 30: f = 9.742235e-01 f-delta = 1.3e-04
 Iter 31: f = 9.743326e-01 f-delta = 1.1e-04
 Iter 32: f = 9.744253e-01 f-delta = 9.3e-05
 Final f = 9.744253e-01 
Elapsed time is 0.054310 seconds.

The cp_orth_als method does not fare as well. The standard CP-ALS method guarantees that the fit (f) is non-decreasing. But the CP-ORTH-ALS does not have that property, and we can see that the f-value actually decreases in some steps due to the orthogonalization.

rng('default')
tic
M = cp_orth_als(X,3);
toc

CP_OrthALS:
Orthogonalized, Iter  1: f = 5.757392e-01 f-delta = 5.8e-01
Orthogonalized, Iter  2: f = 5.255027e-01 f-delta = 5.0e-02
Orthogonalized, Iter  3: f = 5.293016e-01 f-delta = 3.8e-03
Orthogonalized, Iter  4: f = 5.321295e-01 f-delta = 2.8e-03
Orthogonalized, Iter  5: f = 5.235270e-01 f-delta = 8.6e-03
Orthogonalized, Iter  6: f = 5.033360e-01 f-delta = 2.0e-02
Orthogonalized, Iter  7: f = 5.809724e-01 f-delta = 7.8e-02
Orthogonalized, Iter  8: f = 6.332273e-01 f-delta = 5.2e-02
Orthogonalized, Iter  9: f = 6.466917e-01 f-delta = 1.3e-02
Orthogonalized, Iter 10: f = 6.506298e-01 f-delta = 3.9e-03
Orthogonalized, Iter 11: f = 6.518205e-01 f-delta = 1.2e-03
Orthogonalized, Iter 12: f = 6.521794e-01 f-delta = 3.6e-04
Orthogonalized, Iter 13: f = 6.522875e-01 f-delta = 1.1e-04
Orthogonalized, Iter 14: f = 6.523201e-01 f-delta = 3.3e-05
 Final f = 6.523201e-01 
Elapsed time is 0.030349 seconds.

Running cp_orth_als with just 10 iterations of orthogonaliztion speeds starts off with the same problem but recovers once it resumes regular ALS iterations.

rng('default')
tic
M = cp_orth_als(X,3,'stop_orth',10);
toc

CP_OrthALS:
Orthogonalized, Iter  1: f = 5.757392e-01 f-delta = 5.8e-01
Orthogonalized, Iter  2: f = 5.255027e-01 f-delta = 5.0e-02
Orthogonalized, Iter  3: f = 5.293016e-01 f-delta = 3.8e-03
Orthogonalized, Iter  4: f = 5.321295e-01 f-delta = 2.8e-03
Orthogonalized, Iter  5: f = 5.235270e-01 f-delta = 8.6e-03
Orthogonalized, Iter  6: f = 5.033360e-01 f-delta = 2.0e-02
Orthogonalized, Iter  7: f = 5.809724e-01 f-delta = 7.8e-02
Orthogonalized, Iter  8: f = 6.332273e-01 f-delta = 5.2e-02
Orthogonalized, Iter  9: f = 6.466917e-01 f-delta = 1.3e-02
Orthogonalized, Iter 10: f = 6.506298e-01 f-delta = 3.9e-03
Not Orthogonalized, Iter 11: f = 9.048254e-01 f-delta = 2.5e-01
Not Orthogonalized, Iter 12: f = 9.253369e-01 f-delta = 2.1e-02
Not Orthogonalized, Iter 13: f = 9.308225e-01 f-delta = 5.5e-03
Not Orthogonalized, Iter 14: f = 9.342883e-01 f-delta = 3.5e-03
Not Orthogonalized, Iter 15: f = 9.373102e-01 f-delta = 3.0e-03
Not Orthogonalized, Iter 16: f = 9.401759e-01 f-delta = 2.9e-03
Not Orthogonalized, Iter 17: f = 9.429342e-01 f-delta = 2.8e-03
Not Orthogonalized, Iter 18: f = 9.455882e-01 f-delta = 2.7e-03
Not Orthogonalized, Iter 19: f = 9.481328e-01 f-delta = 2.5e-03
Not Orthogonalized, Iter 20: f = 9.505615e-01 f-delta = 2.4e-03
Not Orthogonalized, Iter 21: f = 9.528681e-01 f-delta = 2.3e-03
Not Orthogonalized, Iter 22: f = 9.550467e-01 f-delta = 2.2e-03
Not Orthogonalized, Iter 23: f = 9.570921e-01 f-delta = 2.0e-03
Not Orthogonalized, Iter 24: f = 9.590004e-01 f-delta = 1.9e-03
Not Orthogonalized, Iter 25: f = 9.607688e-01 f-delta = 1.8e-03
Not Orthogonalized, Iter 26: f = 9.623965e-01 f-delta = 1.6e-03
Not Orthogonalized, Iter 27: f = 9.638843e-01 f-delta = 1.5e-03
Not Orthogonalized, Iter 28: f = 9.652348e-01 f-delta = 1.4e-03
Not Orthogonalized, Iter 29: f = 9.664526e-01 f-delta = 1.2e-03
Not Orthogonalized, Iter 30: f = 9.675437e-01 f-delta = 1.1e-03
Not Orthogonalized, Iter 31: f = 9.685153e-01 f-delta = 9.7e-04
Not Orthogonalized, Iter 32: f = 9.693755e-01 f-delta = 8.6e-04
Not Orthogonalized, Iter 33: f = 9.701332e-01 f-delta = 7.6e-04
Not Orthogonalized, Iter 34: f = 9.707974e-01 f-delta = 6.6e-04
Not Orthogonalized, Iter 35: f = 9.713772e-01 f-delta = 5.8e-04
Not Orthogonalized, Iter 36: f = 9.718812e-01 f-delta = 5.0e-04
Not Orthogonalized, Iter 37: f = 9.723180e-01 f-delta = 4.4e-04
Not Orthogonalized, Iter 38: f = 9.726954e-01 f-delta = 3.8e-04
Not Orthogonalized, Iter 39: f = 9.730206e-01 f-delta = 3.3e-04
Not Orthogonalized, Iter 40: f = 9.733004e-01 f-delta = 2.8e-04
Not Orthogonalized, Iter 41: f = 9.735405e-01 f-delta = 2.4e-04
Not Orthogonalized, Iter 42: f = 9.737463e-01 f-delta = 2.1e-04
Not Orthogonalized, Iter 43: f = 9.739224e-01 f-delta = 1.8e-04
Not Orthogonalized, Iter 44: f = 9.740731e-01 f-delta = 1.5e-04
Not Orthogonalized, Iter 45: f = 9.742018e-01 f-delta = 1.3e-04
Not Orthogonalized, Iter 46: f = 9.743117e-01 f-delta = 1.1e-04
Not Orthogonalized, Iter 47: f = 9.744056e-01 f-delta = 9.4e-05
 Final f = 9.744056e-01 
Elapsed time is 0.065581 seconds.

Orthogonalized Alternating least squares for CANDECOMP/PARAFAC (CP) Decomposition

Contents

Recommendation

Example performance on noise-free problem with nearly orthogonal matrices

Example performance on Amino Acids test problem.